高中数学学科知识与教学能力试题(三)
考试总分:150分
考试类型:模拟试题
作答时间:120分钟
已答人数:373
试卷答案:有
试卷介绍: 高中数学学科知识与教学能力试题(三)为大家带来了非常多的高中数学学科知识与教学能力知识点题目,不要错过哦。
试卷预览
-
1. ( )是中国古典数学最重要的著作,分为方田、粟米、衰分、少广、商功、均输、盈不足、方程及勾股九章。
A《九章算术》
B《孙子算经》
C《数书九章》
D《代数学》
-
2.
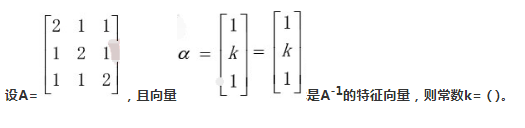
A1
B-2
C-1
D1 或-2
-
3.
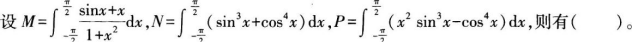
AM<N<P
BN<P<M
CM<P<N
DP<M<N
-
4. 高中数学课程是义务教育阶段后普通高级中学的主要课程,具有()。
A基础性、选择性和发展性
B基础性、选择性和实践性
C基础性、实践性和创新性
D基础性、选择性和普适性
-
5. 在讲解“垂线”一课时,教师自制教具,将两根木条钉在一起并固定其中一根木条a,转动木条b,让学生观察,从而导入新课。这种导入方式属于()。
A实例导入
B直观导入
C悬念导入
D故事导入
-
1.
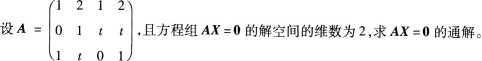
-
2.

-
3. 设随机变量X1,X2,X3,X4相互独立,且有E(Xi)=i,D(Xi)=5-i,i=1,2,3,4。设Y=

-
4. 数学学习评价要求重视过程评价,你能否对实施过程评价提出一些建议?
-
5. 简述数据分析的主要过程。
-
1. 设f(x),g(x)在[0,1]上的导数连续,且ƒ(0)=0,ƒ´(x)≥0,g´(x)≥0。证明:对任何a∈[0,1],有
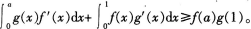
-
1. 《普通高中数学课程标准(实验)》指出:“注重数学知识与实际的联系,发展学生的应用意识和能力”“在数学教学中,应注重发展学生的应用意识”,请叙述如何发展高中生的应用意识和能力,并举例说明。
-
1. 上课时,教师用几何画板任意画了一个锐角,提出问题1:任意画一个锐角a,借助三角板,找出sina,cosa,tana的近似值。然后走进学生中间,观察他们的学习行为,结果发现,有一部分同学画出角之后,一片茫然,教师又不愿意把结果告诉学生,提示同桌的两位同学可以商量一下,并提示完成的同学举手示意,以便教师了解情况,结果举手的人很少。之后,教师提问一位举手的学生,问:“你是怎么做的?”她要求上黑板,教师非常赞成。她在黑板上画出一个直角三角形,并不熟练地写出一个锐角的正弦是它的对边比斜边以及余弦、正切等三个三角函数。之后,教师又与学生讨论了问题2:能否把某条线段画成单位长,有些三角函数值不用计算就可以得到?学生一致认为把斜边长画成单位长比较好,为“单位圆定义法”做必要的铺垫。接着讨论问题3:锐角三角函数sina作为一个函数,自变量以及与之对应的函数值分别是什么?在教师类比正方形的面积S=a2的提示下,学生说出锐角三角函数中自变量以及与之对应的函数值分别是角、比值。最后讨论问题4:你产生过这个疑问吗,三角函数只有这三个?有学生举手,表示想过这个问题,应该是六个,另外三个可以把现有的三个作倒数得到。至此,时间已经过去20多分钟。 问题:
(1)案例中教师上课过程出现了问题,请说出问题出在哪里?
(2)针对该教师的问题,你认为他该怎么改进教学。
-
1. “两角差的余弦公式”是高中数学教材中的重要公式,只有对两角差的余弦有了认识,才能够以此为基础推导其他三角恒等变换公式。这是一个逻辑推理过程,也是一个认识三角函数式的特征,体会三角恒等变换特点的过程。请完成下列问题:
(1)设计“两角差的余弦公式”的教学目标;
(2)写出“两角差的余弦公式”的教学重点和难点;
(3)-写出“两角差的余弦公式”的探究过程(要求使学生意识到,向量方法可能是解决问题的工具)。
相关试卷
相关题库