感谢您信任并使用聚题库系统。我们深知个人信息和隐私保护的重要性,为了更好地保护您的个人权益,在使用产品前请充分阅读并理解《用户服务协议》和 《隐私协议》 。
长沙聚优教育咨询有限公司(以下简称“长沙聚优”)在此特别提醒您在使用相关服务前,请认真阅读协议条款内容,确保您充分理解协议中各条款,特别是免除或者限制责任、法律适用和管辖的条款,以及开通或使用某项服务的单独协议,并选择接受或不接受。如你未满18周岁,请在法定监护人陪同下仔细阅读并充分理解本协议,并征得法定监护人的同意后使用“聚题库”软件及相关服务。除非您接受本协议所有条款,否则您无权注册、登录或使用本协议所涉服务。
隐私权政策适用我们提供的软件、网站、服务,包括但不限于适用于电脑、移动智能终端产品及服务。
本隐私权政策旨在帮助您了解我们会收集哪些数据,为什么收集这些数据、会利用这些数据做什么以及我们如何保护这些数据。了解这些内容,对于您行使个人权利及保护您的个人信息至关重要,请您在使用我们产品或服务前务必抽出时间认真阅读本政策。
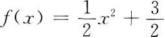
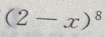 的展开式中,
的展开式中, 的系数是
的系数是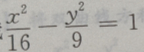 的渐近线的斜率为k,则|k|=()
的渐近线的斜率为k,则|k|=()
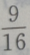
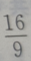
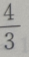
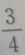
 的展开式是()
的展开式是()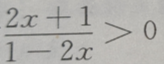 的解集为()
的解集为()
 的定义域是()
的定义域是() AB=120m,求河的宽
AB=120m,求河的宽

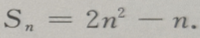 (Ⅰ)求这个数列的通项公式;(Ⅱ)求数列第六项到第十项的和
(Ⅰ)求这个数列的通项公式;(Ⅱ)求数列第六项到第十项的和 (Ⅰ)求f(x)的单调区间;
(Ⅱ)求 f(x)的极值
(Ⅰ)求f(x)的单调区间;
(Ⅱ)求 f(x)的极值 (Ⅰ)写出向量
(Ⅰ)写出向量 和
和 关于基底{a,b,c}的分解式;
(Ⅱ)求证:
关于基底{a,b,c}的分解式;
(Ⅱ)求证: (Ⅲ)求证:
(Ⅲ)求证: