首页 课程学习 题库 APP下载 报名官网入口
注册 帮助中心 合作联系
当前位置：首页 > 考试 > 学历类 > 高职单招 > 数学 >
2023年高职单招每日一练《数学》2月14日

2023年高职单招每日一练《数学》2月14日

考试总分：10分

考试类型：模拟试题

作答时间：60分钟

已答人数：1400

试卷答案：有

试卷介绍： 2023年高职单招每日一练《数学》2月14日专为备考2023年数学考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

开始答题

试卷预览

判断题 单选题 主观题 填空题 简答题
  • 1. 若函数f(x)=3x2+bx-1(b∈R)是偶函数，则f(-1)=2.

    A对

    B错

  • 2. 同时抛三枚硬币，恰有两枚硬币正面朝上的概率是.

    A对

    B错

  • 1. 若a、b、c、，且a>b，c>d，则下列结论正确的是（）

    Aa+c>b+d

    Ba—c>b—d

    Cac>bd

    D

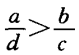
  • 2. 已知平面向量a,b满足|a|=|b|=1,若|3a+2b|=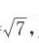,则向量a与b的夹角为（）  

    A

    B

    C

    D

  • 1. 已知等差数列{an}的前n项和Sn且S5=35,S8=104.
    (1)求数列{an}的通项公式；
    (2)若{bn}为等比数列，b1=a2,b2=a3+2,求数列{b,}的公比q及前n项和Tn.
  • 2. 组委会要从小张、小赵、小李、小罗、小王五名志愿者中选派四人分别从事翻译、导游、礼仪、司机四项不同工作，若其中小张和小赵只能从事前两项工作，其余三人均能从事这四项工作，则不同的选派方案共有多少种?
  • 1. 若a>b>0,则a(a+b)（）a2.(填“>”“<”或“=”)
  • 2. 函数的最大值是（）.
  • 1. 已知
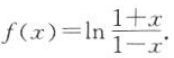
    (1)求f(x)的定义域；
    (2)判断f(x)的奇偶性并证明；
    (3)求f(x)>0的x的取值范围.
  • 2. 解不等式：
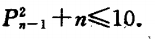
相关试卷
相关题库