首页 课程学习 题库 APP下载 报名官网入口
注册 帮助中心 合作联系
当前位置：首页 > 考试 > 学历类 > 成考高起点 > 数学(文史) >
2023年成考高起点每日一练《数学(文史)》2月10日

2023年成考高起点每日一练《数学(文史)》2月10日

考试总分：10分

考试类型：模拟试题

作答时间：60分钟

已答人数：518

试卷答案：有

试卷介绍： 2023年成考高起点每日一练《数学(文史)》2月10日专为备考2023年数学(文史)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

开始答题

试卷预览

单选题 主观题 填空题
  • 1. 某学校为新生开设了4门选修课程，规定每位新生至少要选其中3门，则一位新生不同的选课方案共有 ( )

    A7种

    B4种

    C5种

    D6种

  • 2. log21/4（）。

    A-2

    B2

    C4

    D-4

  • 3. 不等式x2-2x<0的解集为()。

    A{x∣x＜0或x＞2}

    B{x∣-2＜x＜0}

    C{x∣0＜x＜2}

    D{x∣x＜-2或x＞0}

  • 4. 已知点A(1，-3)，B(0，-3)，C(2，2)，则△ABC的面积为（）

    A2

    B3

    C

    D

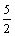
  • 1. 已知等差数列{an}的首项与公差相等，{an}的前n项的和记作Sn，且S20=840．（I）求数列{an}的首项a1及通项公式；（Ⅱ）数列{an}的前多少项的和等于847.
  • 2.
  • 3. 设Sn为数列{an}的前n项和，Sn=3/2(an-1)(n∈N+)，数列{bn}的通项公式为bn=4n+3(n∈N+)。
    (Ⅰ)求数列｛an｝的通项公式；
    (Ⅱ)若di∈{a1，a2，…，an，…}∩{b1，b2，…，bn，…}(i=1，2，…，n，…)，则称数列{dn}为数列{an}与{bn}的公共项，将数列{an}与{bn}的公共项按它们在原数列中的先后顺序排成一个新的数列(dn)，证明{dn}的通项公式为dn=32n+1(n∈N)。
  • 4. （I）求AABC的面积；
    （II）若M为AC边的中点，求BM．
  • 1. 已知平面向量a=(1,2)，b=(-2,3),2a+3b=
  • 2. 过点(1，-2)且与直线3x+y-1=0垂直的直线方程为_______。
相关试卷
相关题库