首页 课程学习 题库 APP下载 报名官网入口
注册 帮助中心 合作联系
当前位置：首页 > 考试 > 学历类 > 成考高起点 > 数学(理) >
2022年成考高起点每日一练《数学(理)》5月23日

2022年成考高起点每日一练《数学(理)》5月23日

考试总分：10分

考试类型：模拟试题

作答时间：60分钟

已答人数：1034

试卷答案：有

试卷介绍： 2022年成考高起点每日一练《数学(理)》5月23日专为备考2022年数学(理)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

开始答题

试卷预览

单选题 主观题 填空题
  • 1. 已知平面向量a=(-2，1)与b=(λ，2)垂直，则λ=（）。

    A4

    B-4

    C-1

    D1

  • 2. 已知三角形的两个顶点是椭圆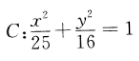的两个焦点，第三个顶点在C上，则该三角形的周长为（）。

    A10

    B20

    C16

    D26

  • 3. 若向量a=(1，1)，b=(1，-1)，则（）

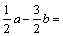    A(1，2)

    B(-1，2)

    C(1，-2)

    D(-1，-2)

  • 4. 若lg5=m，则lg2=()

    A5m

    B1-m

    C2m

    Dm+1

  • 1. 已知{an}是等差数列，且a2=-2，a4=-1. (Ⅰ)求{an}的通项公式； (Ⅱ)求{an}的前n项和Sn.
  • 2. 等差数列{an}中，a1=-393，a2+a3=-768，{bn}是等比数列，q∈(0,1)，b1=2，{bn}的前n项和为20，求：（Ⅰ）求an，bn；
    （Ⅱ）解不等式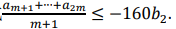
  • 3. 已知函数f(x)=2x3—3x2+2。(Ⅰ)求f'(x)；
    (Ⅱ)求f(x)在区间[-2，2]的最大值与最小值
  • 4. 在△ABC中，BC=a，AC=b，a，b是方程的两个根，且2cos(A+B)=1.求：
    （Ⅰ）角C的度数。
    （Ⅱ）AB的长度。
  • 1. 如果二次函数的图像经过原点和点（-4，0），则该第二次函数图像的对称轴方程
  • 2. 从一个正方体中截去四个三棱锥，得一正三棱锥ABCD，正三棱锥的体积是正方体体积的(  )。
相关试卷
相关题库