首页 课程学习 题库 APP下载 报名官网入口
注册 帮助中心 合作联系
当前位置：首页 > 考试 > 学历类 > 成考高起点 > 数学(理) >
2024年成考高起点每日一练《数学(理)》12月6日

2024年成考高起点每日一练《数学(理)》12月6日

考试总分：10分

考试类型：模拟试题

作答时间：60分钟

已答人数：1953

试卷答案：有

试卷介绍： 2024年成考高起点每日一练《数学(理)》12月6日专为备考2024年数学(理)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

开始答题

试卷预览

单选题 主观题 填空题
  • 1. 棱长等于1的正方体内接于一球体中，则该球的表面积是（）。

    A6π

    B

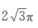
    C3π

    D9π

  • 2. 5名高中毕业生报考3所院校,每人只能报一所院校,则有（）种不同的报名方法  

    A

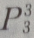
    B

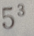
    C

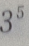
    D

  • 3. “曲线C上的点的坐标都是方程f（x，y）=0的解”是“f（x，y）=0是曲线C的方程”的（）。

    A充分但非必要条件

    B必要但非充分条件

    C充要条件

    D非充分非必要条件

  • 4. i为虚数单位,則i•i2•i3•i4•i5的值为（）。

    A1

    B－1

    Ci

    D－i

  • 1. 求下列函数的最大值、最小值和最小正周期： （1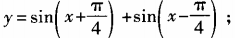）（2）y=6cosx+8sinx
  • 2. 设（0＜α＜π），求tanα的值。
  • 3. 已知数列{an}中，a1=2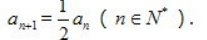， （Ⅰ）求数列{an}的通项公式; （Ⅱ）求数列{an}前5项的和 S5
  • 4. 在△ABC中，B=120°,BC=4,△ABC的面积为，求AC.
  • 1. 已知函数y=a2+bx+c的图像是以(6,-12)为顶点的抛物线，并且与x轴的一个交点坐标是(8,0)，则a=()，b=()，c=()
  • 2. 已知≤0＜2π，且实数x满足log3x=2-cos2θ+sin2θ，则x的最小值是______。  
相关试卷
相关题库