首页 课程学习 题库 APP下载 报名官网入口
注册 帮助中心 合作联系
当前位置：首页 > 考试 > 学历类 > 高职单招 > 数学(中职) >
2024年高职单招每日一练《数学(中职)》10月29日

2024年高职单招每日一练《数学(中职)》10月29日

考试总分：10分

考试类型：模拟试题

作答时间：60分钟

已答人数：215

试卷答案：有

试卷介绍： 2024年高职单招每日一练《数学(中职)》10月29日专为备考2024年数学(中职)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

开始答题

试卷预览

单选题 填空题 简答题
  • 1. 命题“实数a,b,c中至少有2个负数”的否定是（）

    A实数a,b,c中至多有1个负数

    B实数a,b,c中至多有2个负数

    C实数a,b,c中至少有1个负数

    D实数a,b,c都是正数

  • 2. 直线y=2x+1与圆x2+y2-2x+4y=0的位置关系是（）  

    A相切

    B相交且过圆心

    C相离

    D相交且不过圆心

  • 3. 从A,B,C,D四本不同的书中任取两本，则取到A的概率为()  

    A

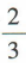
    B

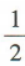
    C

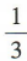
    D

  • 4. 已知等差数列{an}中，a1=-2,公差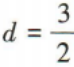则a2与a5的等差中项是()

    A

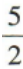
    B

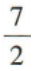
    C

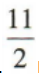
    D6

  • 1. 某医疗机构有4名新冠疫情防控志愿者,现要从这4人中选3个人去3个不同的社区进行志愿服务则不同的安排方法共有（）种.  
  • 2. 若椭圆上一点到两焦点F1(-2,0),F2(2,0)的距离之和为8,则该椭圆的短轴长为()  
  • 3. 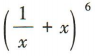的展开式中的常数项是()  
  • 4. 在等差数列{an}中，a1=-23,d=2,则数列{an}中负数项的个数为（）
  • 1. 已知a,b,c分别是△ABC内角A,B,C的对边，且(b-c)2=a2-bc. (1)求角A的大小； (2)若a=3,sinC=2sinB,求△ABC的面积.
  • 2. 已知数列{an}是公比为2的等比数列，且a3是a1与a4-1的等差中项. (1)求{an}的通项公式； (2)
相关试卷
相关题库