首页 课程学习 题库 APP下载 报名官网入口
注册 帮助中心 合作联系
当前位置：首页 > 考试 > 学历类 > 成考高起点 > 数学(理) >
2024年成考高起点每日一练《数学(理)》10月23日

2024年成考高起点每日一练《数学(理)》10月23日

考试总分：10分

考试类型：模拟试题

作答时间：60分钟

已答人数：1952

试卷答案：有

试卷介绍： 2024年成考高起点每日一练《数学(理)》10月23日专为备考2024年数学(理)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

开始答题

试卷预览

单选题 主观题 填空题
  • 1. 设集合M={x||x-2|＜1}，N={x|x＞2}，则M∩N=（）

    A{x|1＜x＜3}

    B{x|x＞2}

    C{x|2＜x＜3}

    D{x|1＜x＜2}

  • 2. 圆x2＋y2＝25上的点到直线5x＋12y－169＝0的距离的最小值是（）。

    A9

    B8

    C7

    D6

  • 3. 函数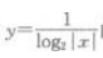定义域为（）。

    A{z|x≠0，x∈R}

    B{x|x≠±1，x∈R}

    C{x|x≠0，x≠±1，x∈R}

    D{x|x∈R}

  • 4. 函数y=sinx+cosx（x∈R）的最小正周期为（）。

    A2π

    Bπ

    C

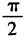
    D

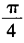
  • 1. 空间有四个点，如果其中任何三点不在同一直线上，可以确定几个平面?  
  • 2. 已知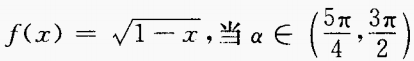时，化简式子f(sin2α)-f(- sin2α)。
  • 3. 已知直线l的斜率为1，l过抛物线C：的焦点，且与C交于A,B两点.(I）求l与C的准线的交点坐标；
    (II）求|AB|.
  • 4. 求函数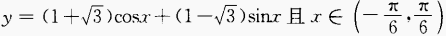上的最大值以及取得这个最大值的x。
  • 1. 的展开式是（）
  • 2. 若A（3，a），B（-4，3）两点间的距离为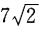，则a=______。
相关试卷
相关题库