2024年高职单招每日一练《数学》10月15日
考试总分：10分
考试类型：模拟试题
作答时间：60分钟
已答人数：497
试卷答案：有
试卷介绍： 2024年高职单招每日一练《数学》10月15日专为备考2024年数学考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。
试卷预览
-
1. y=3tanx的最小正周期为3π。（）
A对
B错
-
2. 已知圆锥的底面半径为2cm，高为1cm，则圆锥的侧面积是14.04平方厘米。()
A对
B错
-
1. 下列问题是组合问题，还是排列问题（）
(1)设集合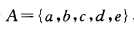
，则集合A有多少个含有3个元素的子集.
(2)某铁路线上有5个车站，则这条铁路线上共需准备多少种车票？
(3)5名同学约定，假期内互通一封信告诉对方自己的情况，共需写多少封？
(4)(3)中的5名同学若互通一次电话告诉对方自己的情况，共需打多少次电话？A(1)(2)(3)都是排列问题
B(1)(2)(3)(4)都是组合问题
C(1)(2)是排列问题；（3)(4)是组合问题
D(1)(4)是组合问题；（2)(3)是排列问题
-
2. 不等式组的解集在数轴上表示如图所示，则该不等式组的解集为()
A2＜x＜4
Bx＞4
Cx＜2
Dx＞2
-
1. 下列四个命题中正确的是（）
A与圆有公共点的直线是该圆的切线
B垂直于圆的半径的直线是该圆的切线
C到圆心的距离等于半径的直线是该圆的切线
D过圆直径的端点，垂直于此直径的直线是该圆的切线
-
2. 列命题中正确的个数是( )
A若a，b，c成等差数列，则a2，b2，c2一定成等差数列；
B若a，b，c成等差数列，则2a,2b,2c可能成等差数列；
C若a，b，c成等差数列，则ka＋2，kb＋2，kc＋2一定成等差数列；
D若a，b，c成等差数列，则1/a，1/b，1/c可能成等差数列．
-
1. 已知函数f(x)=log3(3x—1).(1)求函数f(x)的定义域；
(2)若f(x)<1,求x的取值范围.
-
2. 已知两直线
,当m为何值时，l1与l2: (1)相交；(2)平行；(3)重合.
-
1. 设
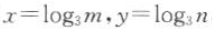,其中m,n是正实数，则mn=（）.
-
2. 从五名学生中选出四名参加数学、物理、生物、化学竞赛，其中甲不参加物理和化学竞赛，则不同的参赛方案的种类是_______.
相关试卷
相关题库
