2024年成考高起点每日一练《数学(理)》9月11日
考试总分：10分
考试类型：模拟试题
作答时间：60分钟
已答人数：227
试卷答案：有
试卷介绍： 2024年成考高起点每日一练《数学(理)》9月11日专为备考2024年数学(理)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。
试卷预览
-
1. 参数方程
（
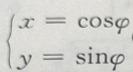为参数）表示的图形为（）A直线
B圆
C椭圆
D双曲线
-
2. 对满足a>b的任意两个非零实数，下列不等式成立的是（）
A
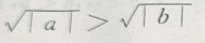
B
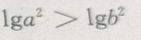
C
D
-
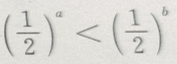
3. 一个袋子中装有标号分别为1，2，3，4的四个球，采用有放回的方式从袋中摸球两次，每次摸出一个球，则恰有一次摸出2号球的概率为（）。
A
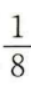
B
C
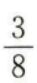
D
-
4. 抛物线y2＝4x上一点P到焦点F的距离是10，则点P坐标是（）。
A（9，6）
B（9，±6）
C（6，9）
D（±6，9）
-
1. （1）已知tanα=
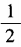，求cot2α的值； （2）已知tan2α=1，求tanα的值。
-
2. 设A1A2A3A4A5A6为正六边形，如图
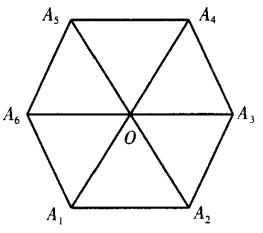，O为它的中心。 （1）求证： 
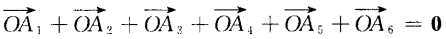（2）
-
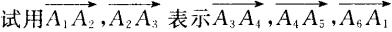
3. 求下列函数的定义域： （1）
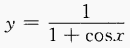
（2）
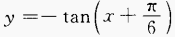
（3）
-
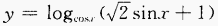
4. 设函数f(x)=
(Ⅰ)求f(x)的单调区间;
(Ⅱ)求 f(x)的极值
-
1. 一个问题在1小时内，甲能独立解决的概率是0.5，乙能独立解决的概率是0.4，两人在1小时内解决问题的概率是______。
-
2.
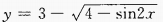的值域是______。
相关试卷
-
2022年成考高起点每日一练《数学(理)》11月17日1036人做过
-
2022年成考高起点每日一练《数学(理)》11月18日527人做过
-
2022年成考高起点每日一练《数学(理)》11月19日1715人做过
-
2022年成考高起点每日一练《数学(理)》11月20日1492人做过
-
2022年成考高起点每日一练《数学(理)》11月21日938人做过
-
2022年成考高起点每日一练《数学(理)》11月22日1912人做过
-
2022年成考高起点每日一练《数学(理)》11月23日301人做过
-
2022年成考高起点每日一练《数学(理)》11月24日1433人做过
-
2022年成考高起点每日一练《数学(理)》11月25日182人做过
-
2022年成考高起点每日一练《数学(理)》11月26日1372人做过
相关题库
