2024年成考高起点每日一练《数学(理)》9月2日
考试总分：10分
考试类型：模拟试题
作答时间：60分钟
已答人数：1483
试卷答案：有
试卷介绍： 2024年成考高起点每日一练《数学(理)》9月2日专为备考2024年数学(理)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。
试卷预览
-
1. 下列函数中，为奇函数的是（）
A
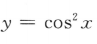
B
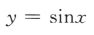
C
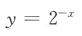
D
-
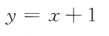
2. 抛物线y＝ax2（a＜0）的焦点坐标是（）。
A
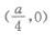
B
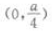
C
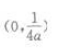
D
-
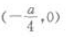
3. 5名高中毕业生报考3所院校,每人只能报一所院校,则有（）种不同的报名方法
A
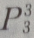
B
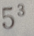
C
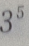
D
-
4. 已知直线l：3x-2y-5=0，圆C：
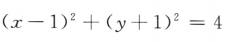，则C上到l的距离为1的点共有（）A1个
B2个
C3个
D4个
-
1. 设函数f(x)=xlnx+x.(I）求曲线y=f(x）在点（(1,f(1))处的切线方程；
(II）求f（x）的极值．
-
2. 已知直线l的斜率为1，l过抛物线C：
的焦点，且与C交于A,B两点.(I）求l与C的准线的交点坐标；
(II）求|AB|.
-
3. 设函数
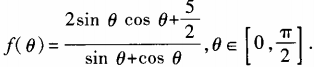（1）求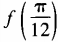
；（2）求函数f（θ）最小值。
-
4. 某气象预报站天气预报的准确率为80%，计算（1）5次预报中恰有4次准确的概率； （2）5次中至少有次准确的概率.(计算结果保留两个有效数字).
-
1. 已知
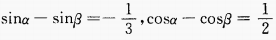，则
=______。
-
2. 函数y=-x2+ax图像的对称轴为x=2，则a=______。
相关试卷
相关题库
