2024年高职单招每日一练《数学》8月8日
考试总分：10分
考试类型：模拟试题
作答时间：60分钟
已答人数：1468
试卷答案：有
试卷介绍： 2024年高职单招每日一练《数学》8月8日专为备考2024年数学考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。
试卷预览
-
1. 函数
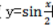的最小正周期是
。（）
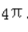A对
B错
-
2. 长度相等的两条弧是等弧。（）
A对
B错
-
1. 函数
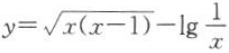的定义域是().A
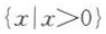
B
C
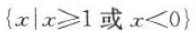
D
-
2. 已知圆C的标准方程是（x-2）2+（y-3）2=4，则点P（3，2）（）
A在圆C外
B在圆C内
C在圆C上
D不能确定
-
1. 已知函数y=1/2sin2x则（）
A函数最大值为2
B函数最大值为1/2
C周期
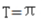
D周期
-
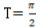
2. 列命题中正确的个数是( )
A若a，b，c成等差数列，则a2，b2，c2一定成等差数列；
B若a，b，c成等差数列，则2a,2b,2c可能成等差数列；
C若a，b，c成等差数列，则ka＋2，kb＋2，kc＋2一定成等差数列；
D若a，b，c成等差数列，则1/a，1/b，1/c可能成等差数列．
-
1. 已知等差数列{an}的前n项和Sn且S5=35,S8=104.
(1)求数列{an}的通项公式；
(2)若{bn}为等比数列，b1=a2,b2=a3+2,求数列{b,}的公比q及前n项和Tn.
-
2. 已知两直线
,当m为何值时，l1与l2: (1)相交；(2)平行；(3)重合.
-
1. 学校文艺队每个队员唱歌、跳舞至少会一门，已知会唱歌的有5人，会跳舞的有7人，现从中选3人，且至少要有一位既会唱歌又会跳舞的概率是
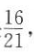,则该队有（）人.
-
2. 函数
的单调递减区间是______.
相关试卷
相关题库
