2024年成考高起点每日一练《数学(理)》5月11日
考试总分：10分
考试类型：模拟试题
作答时间：60分钟
已答人数：429
试卷答案：有
试卷介绍： 2024年成考高起点每日一练《数学(理)》5月11日专为备考2024年数学(理)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。
试卷预览
-
1.
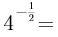（ ）A-2
B
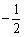
C
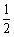
D2
-
2. 方程
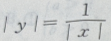的图像是下图中的（）
A
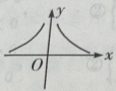
B
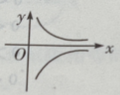
C
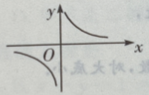
D
-
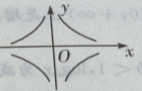
3. 给出下列两个命题：①如果一条直线与一个平面垂直，则该直线与该平面内的任意一条直线垂直②以二面角的棱上任意一点为端点，在二面角的两个面内分别作射线，则这两条射线所成的角为该二面角的平面角.则（）
A①②都为真命题
B①为真命题，②为假命题
C①为假命题，②为真命题
D①②都为假命题
-
4. 袋中有6个球，其中4个红球，2个白球，从中随机取出2个球，则其中恰有1个红球的概率为（）
A
B
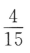
C
D
-
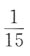
1. 已知直线l的斜率为1，l过抛物线C：
的焦点，且与C交于A,B两点.(I）求l与C的准线的交点坐标；
(II）求|AB|.
-
2. 设函数f(x)=xlnx+x.(I）求曲线y=f(x）在点（(1,f(1))处的切线方程；
(II）求f（x）的极值．
-
3. 设函数f(x)=
(Ⅰ)求f(x)的单调区间;
(Ⅱ)求 f(x)的极值
-
4. 为了测河的宽,在岸边选定两点A和B,望对岸标记物C,测得
AB=120m,求河的宽
-
1. 过点（2，0）作圆x2+y2=1的切线，切点的横坐标为（）。
-
2. 曲线y=在点(1，1)处的切线方程是______。
相关试卷
-
2023年成考高起点每日一练《数学(理)》11月5日1497人做过
-
2023年成考高起点每日一练《数学(理)》11月6日1409人做过
-
2023年成考高起点每日一练《数学(理)》11月7日231人做过
-
2023年成考高起点每日一练《数学(理)》11月8日1344人做过
-
2023年成考高起点每日一练《数学(理)》11月9日505人做过
-
2023年成考高起点每日一练《数学(理)》11月10日429人做过
-
2023年成考高起点每日一练《数学(理)》11月11日467人做过
-
2023年成考高起点每日一练《数学(理)》11月12日1101人做过
-
2023年成考高起点每日一练《数学(理)》11月13日476人做过
-
2023年成考高起点每日一练《数学(理)》11月14日1877人做过
相关题库
