首页 课程学习 题库 APP下载 报名官网入口
注册 帮助中心 合作联系
当前位置：首页 > 考试 > 学历类 > 成考高起点 > 数学(理) >
2024年成考高起点每日一练《数学(理)》1月31日

2024年成考高起点每日一练《数学(理)》1月31日

考试总分：10分

考试类型：模拟试题

作答时间：60分钟

已答人数：1582

试卷答案：有

试卷介绍： 2024年成考高起点每日一练《数学(理)》1月31日专为备考2024年数学(理)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

开始答题

试卷预览

单选题 主观题 填空题
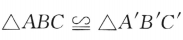  • 1. 设甲：；乙：.则（）

    A甲是乙的必要条件但不是充分条件

    B甲是乙的充分条件但不是必要条件

    C甲是乙的充要条件

    D甲既不是乙的充分条件也不是乙的必要条件

  • 2. 设A、B、C是三个随机事件,用A、B、C的运算关系（）表示事件:B、C都发生,而A不发生  

    A

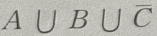
    B

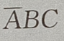
    C

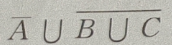
    D

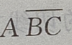
  • 3. 从椭圆与x轴额右交点看短轴两端点的视角为60°的椭圆的离心率（）  

    A

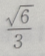
    B

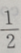
    C1

    D

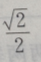
  • 4. 圆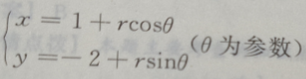的圆心在（）点上  

    A(1,-2)

    B(0,5)

    C(5,5)

    D(0,0)

  • 1. 在正四棱柱ABCD-A'B'C'D'中， （Ⅰ）写出向量关于基底{a,b,c}的分解式 （Ⅱ）求证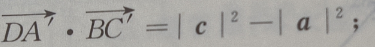： （Ⅲ）求证：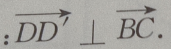  
  • 2. 某工厂每月生产x台游戏机的收入为R(x)=+130x-206(百元)，成本函数为C(x)=50x+100(百元)，当每月生产多少台时,获利润最大?最大利润为多少?  
  • 3. 设函数f(x)=xlnx+x.(I）求曲线y=f(x）在点（(1,f(1))处的切线方程；
    (II）求f（x）的极值．
  • 4. 设函数f(x)= (Ⅰ)求f(x)的单调区间; (Ⅱ)求 f(x)的极值
  • 1. 的展开式是（）
  • 2. 椭圆的中心在原点，一个顶点和一个焦点分别是直线x+3y-6与两坐标轴的交点,则此椭圆的标准方程为（）  
相关试卷
相关题库