首页 课程学习 题库 APP下载 报名官网入口
注册 帮助中心 合作联系
当前位置：首页 > 考试 > 学历类 > 成考高起点 > 数学(理) >
2024年成考高起点每日一练《数学(理)》1月27日

2024年成考高起点每日一练《数学(理)》1月27日

考试总分：10分

考试类型：模拟试题

作答时间：60分钟

已答人数：1143

试卷答案：有

试卷介绍： 2024年成考高起点每日一练《数学(理)》1月27日专为备考2024年数学(理)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

开始答题

试卷预览

单选题 主观题 填空题
  • 1. 某类灯泡使用时数在1000小时以上的概率为0.2,三个灯泡在使用1000小时以后最多只有一个坏的概率为（）

    A0.008

    B0.104

    C0.096

    D1

  • 2. 设集合A={0,1}，B={0,1,2}，则A∩B=（）  

    A{1,2}

    B{0,2}

    C{0,1}

    D{0,1,2}

  • 3. 过点P(2,3)且在两轴上截距相等的直线方程为()  

    A

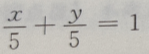
    B

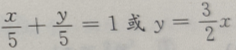
    Cx+y=5

    D

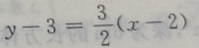
  • 4. 对满足a>b的任意两个非零实数，下列不等式成立的是（）  

    A

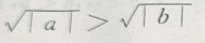
    B

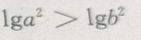
    C

    D

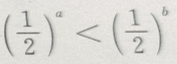
  • 1. 已知直线l的斜率为1，l过抛物线C：的焦点，且与C交于A,B两点.(I）求l与C的准线的交点坐标；
    (II）求|AB|.
  • 2. 已知数列的前n项和 求证：是等差数列，并求公差和首项。  
  • 3. 建筑一个容积为8000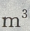,深为6m的长方体蓄水池，池壁每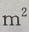的造价为15元，池底每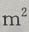的造价为30元。（I）把总造价y(元)表示为长x(m)的函数；（Ⅱ）求函数的定义域  
  • 4. 设函数f(x)=xlnx+x.(I）求曲线y=f(x）在点（(1,f(1))处的切线方程；
    (II）求f（x）的极值．
  • 1. 不等式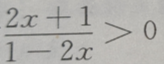的解集为（）  
  • 2. 的展开式是（）
相关试卷
相关题库