首页 课程学习 题库 APP下载 报名官网入口
注册 帮助中心 合作联系
当前位置：首页 > 考试 > 学历类 > 成考高起点 > 数学(理) >
2024年成考高起点每日一练《数学(理)》1月17日

2024年成考高起点每日一练《数学(理)》1月17日

考试总分：10分

考试类型：模拟试题

作答时间：60分钟

已答人数：1841

试卷答案：有

试卷介绍： 2024年成考高起点每日一练《数学(理)》1月17日专为备考2024年数学(理)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

开始答题

试卷预览

单选题 主观题 填空题
  • 1. 下列函数中，为减函数的是（）

    A

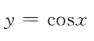
    B

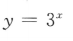
    C

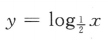
    D

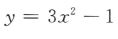
  • 2. 过点P(2,3)且在两轴上截距相等的直线方程为()  

    A

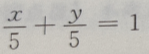
    B

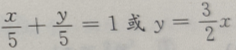
    Cx+y=5

    D

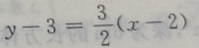
  • 3. 袋中有6个球，其中4个红球，2个白球，从中随机取出2个球，则其中恰有1个红球的概率为（）

    A

    B

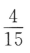
    C

    D

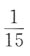
  • 4. 过点（-2，2）与直线x+3y-5=0平行的直线是（）

    Ax+3y-4=0

    B3x+y+4=0

    Cx+3y+8=0

    D3x-y+8=0

  • 1. 已知a,b,c成等差数列，a,b,c+1成等比数列．若b=6，求a和c．
  • 2. 设函数f(x)=xlnx+x.(I）求曲线y=f(x）在点（(1,f(1))处的切线方程；
    (II）求f（x）的极值．
  • 3. 在正四棱柱ABCD-A'B'C'D'中， （Ⅰ）写出向量关于基底{a,b,c}的分解式 （Ⅱ）求证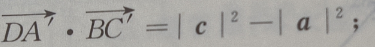： （Ⅲ）求证：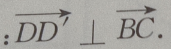  
  • 4. 在正四棱柱ABCD-A'B'C'D'中， （Ⅰ）写出向量和关于基底{a,b,c}的分解式; （Ⅱ）求证： （Ⅲ）求证：  
  • 1. 若平面向量a=(x,1),b=(1,-2),且a//b,则x=（）  
  • 2. 函数的定义域是（）
相关试卷
相关题库