2024年成考高起点每日一练《数学(理)》1月14日
考试总分：10分
考试类型：模拟试题
作答时间：60分钟
已答人数：205
试卷答案：有
试卷介绍： 2024年成考高起点每日一练《数学(理)》1月14日专为备考2024年数学(理)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。
试卷预览
-
1. 已知
，则sin2α=（）A
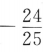
B
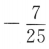
C
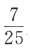
D
-
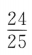
2. 对满足a>b的任意两个非零实数，下列不等式成立的是（）
A
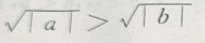
B
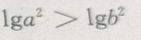
C
D
-
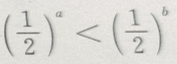
3. 已知向量a=(3,4),向量 b=(0,-2),则cos的值为（）
A
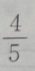
B
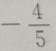
C
D
-
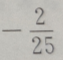
4. 已知α∩β=a，b⊥β，b在α内的射影是b’，那么b'和α的关系是（）
Ab'//α
Bb'⊥α
Cb'与α是异面直线
Db'与α相交成锐角
-
1. 已知等差数列前n项和
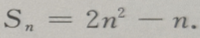（Ⅰ）求这个数列的通项公式;（Ⅱ）求数列第六项到第十项的和
-
2. 设函数f(x)=
(Ⅰ)求f(x)的单调区间;
(Ⅱ)求 f(x)的极值
-
3. 在正四棱柱ABCD-A'B'C'D'中，
（Ⅰ）写出向量
和
关于基底{a,b,c}的分解式;
（Ⅱ）求证：
（Ⅲ）求证：
-
4. 设函数f(x)=xlnx+x.(I）求曲线y=f(x）在点（(1,f(1))处的切线方程；
(II）求f（x）的极值．
-
1. 不等式
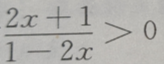的解集为（）
-
2. 函数
的定义域是（）
相关试卷
-
2023年成考高起点每日一练《数学(理)》4月18日1476人做过
-
2023年成考高起点每日一练《数学(理)》4月19日1434人做过
-
2023年成考高起点每日一练《数学(理)》4月20日415人做过
-
2023年成考高起点每日一练《数学(理)》4月21日300人做过
-
2023年成考高起点每日一练《数学(理)》4月22日1440人做过
-
2023年成考高起点每日一练《数学(理)》4月23日584人做过
-
2023年成考高起点每日一练《数学(理)》4月24日861人做过
-
2023年成考高起点每日一练《数学(理)》4月25日946人做过
-
2023年成考高起点每日一练《数学(理)》4月26日1840人做过
-
2023年成考高起点每日一练《数学(理)》4月27日614人做过
相关题库
