首页 课程学习 题库 APP下载 报名官网入口
注册 帮助中心 合作联系
当前位置：首页 > 考试 > 学历类 > 高职单招 > 数学 >
2024年高职单招每日一练《数学》1月6日

2024年高职单招每日一练《数学》1月6日

考试总分：10分

考试类型：模拟试题

作答时间：60分钟

已答人数：1960

试卷答案：有

试卷介绍： 2024年高职单招每日一练《数学》1月6日专为备考2024年数学考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

开始答题

试卷预览

判断题 单选题 多选题 主观题 填空题
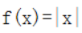  • 1. 函数与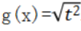表示同一个函数。（）  

    A对

    B错

  • 2. 一名学生在七次数学测验中所得分数分别为85,82,86,82,91,86,82,则此学生所得分数的众数是86。()  

    A对

    B错

  • 1. 若f（x）对于任意实数x都有2f（x）-f（1/x）=2x+1，则f（1/2）=（）  

    A1

    B2

    C5

    D3

  • 2. 用配方法解一元二次方程x2-4x-3=0，下列变形正确的是（）  

    A（x-4）2=-19

    B（x-4）2=28

    C（x-2）2=7

    D（x-2）2=-3

  • 1. 已知数列{3n-1}，下面选项正确的是（）  

    A这个数列是公比为3的等比数列

    B这个数列是公差为3的等差数列

    C这个数列的第5项是14

    D20是这个数列的第7项

  • 2. 列命题中正确的个数是(　　)  

    A若a，b，c成等差数列，则a2，b2，c2一定成等差数列；

    B若a，b，c成等差数列，则2a,2b,2c可能成等差数列；

    C若a，b，c成等差数列，则ka＋2，kb＋2，kc＋2一定成等差数列；

    D若a，b，c成等差数列，则1/a，1/b，1/c可能成等差数列．

  • 1. 已知等差数列{an}的前n项和Sn且S5=35,S8=104.
    (1)求数列{an}的通项公式；
    (2)若{bn}为等比数列，b1=a2,b2=a3+2,求数列{b,}的公比q及前n项和Tn.
  • 2. 已知函数f(x)=log3(3x—1).(1)求函数f(x)的定义域；
    (2)若f(x)<1,求x的取值范围.
  • 1. 在菱形ABCD中，（）  
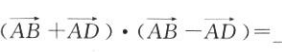  • 2. 设a、b为非零向量，若|a+b|=|a|+|b|，则a的方向与b的方向必定_____.  
相关试卷
相关题库