首页 课程学习 题库 APP下载 报名官网入口
注册 帮助中心 合作联系
当前位置：首页 > 考试 > 学历类 > 成考高起点 > 数学(理) >
2023年成考高起点每日一练《数学(理)》12月25日

2023年成考高起点每日一练《数学(理)》12月25日

考试总分：10分

考试类型：模拟试题

作答时间：60分钟

已答人数：810

试卷答案：有

试卷介绍： 2023年成考高起点每日一练《数学(理)》12月25日专为备考2023年数学(理)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

开始答题

试卷预览

单选题 主观题 填空题
  • 1. 已知直线l：3x-2y-5=0，圆C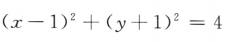：，则C上到l的距离为1的点共有（）

    A1个

    B2个

    C3个

    D4个

  • 2. 若tanα=3，则

    A-2

    B

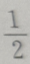
    C2

    D-4

  • 3. 若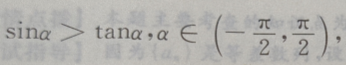则（）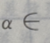

    A

    B

    C

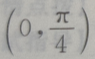
    D

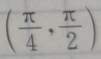
  • 4. 5名高中毕业生报考3所院校,每人只能报一所院校,则有（）种不同的报名方法  

    A

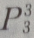
    B

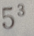
    C

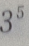
    D

  • 1. 设函数f(x)=xlnx+x.(I）求曲线y=f(x）在点（(1,f(1))处的切线方程；
    (II）求f（x）的极值．
  • 2. 在△ABC中，B=120°,BC=4,△ABC的面积为，求AC.
  • 3. 某工厂每月生产x台游戏机的收入为R(x)=+130x-206(百元)，成本函数为C(x)=50x+100(百元)，当每月生产多少台时,获利润最大?最大利润为多少?  
  • 4. 已知等差数列前n项和 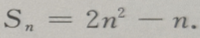（Ⅰ）求这个数列的通项公式;（Ⅱ）求数列第六项到第十项的和
  • 1. 长方体的长、宽、高分别为2,3,6，则该长方体的对角线长为（）
  • 2. 若平面向量a=(x,1),b=(1,-2),且a//b,则x=（）  
相关试卷
相关题库