2023年成考高起点每日一练《数学(理)》9月5日
考试总分：10分
考试类型：模拟试题
作答时间：60分钟
已答人数：1279
试卷答案：有
试卷介绍： 2023年成考高起点每日一练《数学(理)》9月5日专为备考2023年数学(理)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。
试卷预览
-
1. 5名高中毕业生报考3所院校,每人只能报一所院校,则有（）种不同的报名方法
A
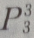
B
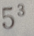
C
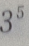
D
-
2. 若
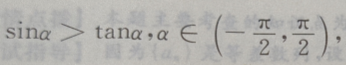则
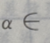（）A
B
C
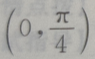
D
-
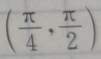
3. 在△ABC中，若lgsinA-lgsinB-lgcos=lg2，则△ABC是（）
A以A为直角的三角形
Bb=c的等腰三角形
C等边三角形
D钝角三角形
-
4. 设A、B、C是三个随机事件,用A、B、C的运算关系（）表示事件:B、C都发生,而A不发生
A
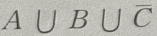
B
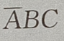
C
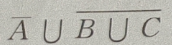
D
-
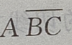
1. 设函数f(x)=xlnx+x.(I）求曲线y=f(x）在点（(1,f(1))处的切线方程；
(II）求f（x）的极值．
-
2. 在正四棱柱ABCD-A'B'C'D'中，
（Ⅰ）写出向量
关于基底{a,b,c}的分解式
（Ⅱ）求证：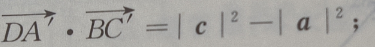
（Ⅲ）求证：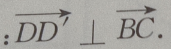
-
3. 已知数列
的前n项和
求证：
是等差数列，并求公差和首项。
-
4. 已知等差数列前n项和
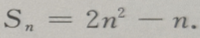（Ⅰ）求这个数列的通项公式;（Ⅱ）求数列第六项到第十项的和
-
1. lg(tan43°tan45°tan47°)=（）
-
2.
的展开式是（）
相关试卷
-
2024年成考高起点每日一练《数学(理)》8月22日437人做过
-
2024年成考高起点每日一练《数学(理)》8月23日1340人做过
-
2024年成考高起点每日一练《数学(理)》8月24日405人做过
-
2024年成考高起点每日一练《数学(理)》8月25日1400人做过
-
2024年成考高起点每日一练《数学(理)》8月26日1210人做过
-
2024年成考高起点每日一练《数学(理)》8月27日133人做过
-
2024年成考高起点每日一练《数学(理)》8月28日1691人做过
-
2024年成考高起点每日一练《数学(理)》8月29日122人做过
-
2024年成考高起点每日一练《数学(理)》8月30日627人做过
-
2024年成考高起点每日一练《数学(理)》8月31日521人做过
相关题库
