2023年高职单招《数学》每日一练试题05月31日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
判断题
1、已知向量a=(x,-3),b=(3,1),若a⊥b,则x=-9.
答 案:错
解 析:若a⊥b,则a·b=0,即3x-3=0,即x=1.
2、已知集合A={-1,0,1,2},B={x|x<0},则A∩B={-1,0}.
答 案:错
解 析:A∩B是集合A和集合B中相同元素的集合,即A∩B={-1).
单选题
1、x、y∈R,则下列命题中,甲是乙的充分不必要条件的命题是()
- A:甲:|x|=|y|,乙:x=y
- B:甲:x=0或y=0,乙:xy=0
- C:甲:x+y=0,乙:x2- y2= 0
- D:甲:(x一3)(y—1)=0,乙:x=3且y=1
答 案:C
解 析:若甲是乙的充分不必要条件,则甲⇒乙为真命题,乙⇒甲为假命题,根据实数的性质,绝对值的性质,不等式的性质逐一分析四个答案,即可得到结论.
A、甲: |x|=|y|,乙: x=y,甲是乙的必要不充分条件
B、甲: x=0或y=0,乙: xy=0,甲是乙的充要条件
C、甲: x+y=0,乙: x2-y2=0,甲是乙的充分不必要条件
D、甲: (x-3)(y-1)=0, 乙: x=3且x=1,甲是乙的既不充分也不必要条件
综上所述,答案: C
2、若函数f(x)= logax(0<a<1)在区间[a,2a]上的最大值是最小值的3倍,则a等于( )
答 案:A
解 析:
利用对数函数的单调性,得出函数在给定区间上的最值,得到关于a的方程,借助于方程思想研究参数的值.
考察对数函数y=logax,(0<a<1)由于(0<a<1),故对数函数y=logax是减函数,
∴函数f(x)=logax(0<a<1)在区间[a,2a]上的最大值是logaa,最小值是loga2a,
∴logaa=3loga(2a),⇒1=3loga2+3⇒a=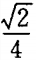
主观题
1、已知两直线 ,当m为何值时,l1与l2: (1)相交;(2)平行;(3)重合.
,当m为何值时,l1与l2: (1)相交;(2)平行;(3)重合.
答 案:(1)当1×3m-(m-2)m2=-m2(m-2)+3m=-m(m-3)(m+1)≠0时,l1与l2相交,即m≠0,m≠3且m≠-1.
(2)当-m(m-3)(m+1)=0且1×2m-(m-2)×6=12-4m≠0时,l1与l2平行,即m=0或m=-1.
(3)当-m(m-3)(m+1)=0且12-4m=0时,l1与l2重合,即m=3.
2、已知等差数列{an}的前n项和Sn且S5=35,S8=104.
(1)求数列{an}的通项公式;
(2)若{bn}为等比数列,b1=a2,b2=a3+2,求数列{b,}的公比q及前n项和Tn.
答 案:(1)
 所以a6=19.则数列{an}的公差
所以a6=19.则数列{an}的公差 ,通项公式为an=a6+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以
,通项公式为an=a6+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以 则
则
填空题
1、设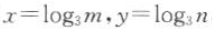 ,其中m,n是正实数,则mn=().
,其中m,n是正实数,则mn=().
答 案:3x+y
解 析:由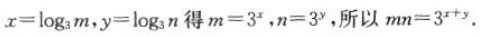
2、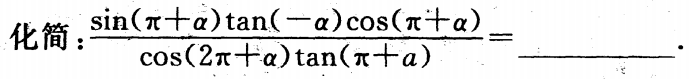
答 案: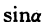
简答题
1、已知集合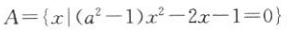 ,且集合A有且只有一个非空子集,求实数a的值.
,且集合A有且只有一个非空子集,求实数a的值.
答 案:由题意可知集合A只有1个元素.当a2-1=0时,a=±1,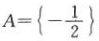 ,满足题意;
,满足题意;
当a2-1≠0时,要使方程(a2-1)x2-2x-1=0有唯一的实根,则(-2)2-4(a2-1)×(-1)=0,解得a=0,此时A={-1},满足题意.
综上所述,满足条件的a的值有-1,0,1.
2、已知双曲线焦点在x轴上,实轴长为2,离心率为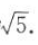 (1)求双曲线的标准方程;
(2)求直线y=x+1被双曲线截得的弦长.
(1)求双曲线的标准方程;
(2)求直线y=x+1被双曲线截得的弦长.
答 案:(1)根据题意可得2a=2,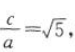 解得a=1,
解得a=1,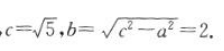 所以双曲线的标准方程为(焦点在x轴)
所以双曲线的标准方程为(焦点在x轴)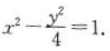 (2)联立方程组组
(2)联立方程组组 将②代入①化简得
将②代入①化简得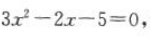 解得
解得 即直线与双曲线的交点坐标为
即直线与双曲线的交点坐标为 两点间的距离
两点间的距离 所以所求弦长
所以所求弦长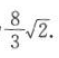
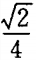

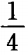
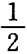
 ,当m为何值时,l1与l2: (1)相交;(2)平行;(3)重合.
,当m为何值时,l1与l2: (1)相交;(2)平行;(3)重合. 
 所以a6=19.则数列{an}的公差
所以a6=19.则数列{an}的公差 ,通项公式为an=a6+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以
,通项公式为an=a6+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以 则
则
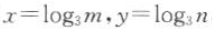 ,其中m,n是正实数,则mn=().
,其中m,n是正实数,则mn=().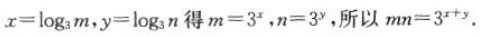
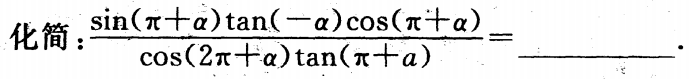
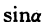
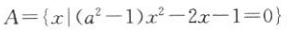 ,且集合A有且只有一个非空子集,求实数a的值.
,且集合A有且只有一个非空子集,求实数a的值.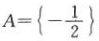 ,满足题意;
,满足题意;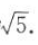 (1)求双曲线的标准方程;
(2)求直线y=x+1被双曲线截得的弦长.
(1)求双曲线的标准方程;
(2)求直线y=x+1被双曲线截得的弦长.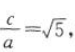 解得a=1,
解得a=1,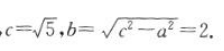 所以双曲线的标准方程为(焦点在x轴)
所以双曲线的标准方程为(焦点在x轴)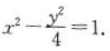 (2)联立方程组组
(2)联立方程组组 将②代入①化简得
将②代入①化简得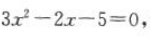 解得
解得 即直线与双曲线的交点坐标为
即直线与双曲线的交点坐标为 两点间的距离
两点间的距离 所以所求弦长
所以所求弦长