2023年高职单招《数学》每日一练试题05月02日
2023-05-02 13:15:46 来源:吉格考试网
2023年高职单招《数学》每日一练试题05月02日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
判断题
1、log39=log3(3×3)=3.
答 案:错
解 析:log39=log332=2.
2、抛物线y2=-8x的焦点坐标是(2,0).
答 案:错
解 析: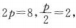 焦点为(一2,0).
焦点为(一2,0).
单选题
1、
- A:A
- B:B
- C:C
- D:D
答 案:A
2、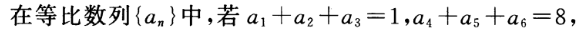 则q等于( )
则q等于( )
- A:-2
- B:2
- C:7/9
- D:-7/9
答 案:B
解 析:设等比数列{an}的公比为q, 由a1+a2+a3=1 ①, a4+a5+a6=q3(a1+a2+a3)=8 ②, ②÷①得:q3=8,∴q=2. 故选:B.
主观题
1、已知函数f(x)=log3(3x—1).(1)求函数f(x)的定义域;
(2)若f(x)<1,求x的取值范围.
答 案:(1)根据题意可得,3x-1>0,解得 所以函数f(x)的定义域是
所以函数f(x)的定义域是 (2)因为f(x)=log3(3x-1)<1=log33,f(x)为定义域上的增函数,所以O<3x-1<3,解得
(2)因为f(x)=log3(3x-1)<1=log33,f(x)为定义域上的增函数,所以O<3x-1<3,解得
 所以x的取值范围是
所以x的取值范围是
2、已知两直线 ,当m为何值时,l1与l2: (1)相交;(2)平行;(3)重合.
,当m为何值时,l1与l2: (1)相交;(2)平行;(3)重合.
答 案:(1)当1×3m-(m-2)m2=-m2(m-2)+3m=-m(m-3)(m+1)≠0时,l1与l2相交,即m≠0,m≠3且m≠-1. (2)当-m(m-3)(m+1)=0且1×2m-(m-2)×6=12-4m≠0时,l1与l2平行,即m=0或m=-1. (3)当-m(m-3)(m+1)=0且12-4m=0时,l1与l2重合,即m=3.
填空题
1、函数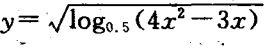 的定义域是_____.
的定义域是_____.
答 案:[-1/4,0)∪(3/4,1]
解 析: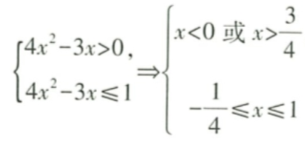
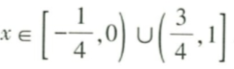
2、函数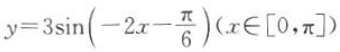 的增区间为().
的增区间为().
答 案: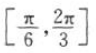
简答题
1、函数f(x)=ax(a>0,且a≠1)在区间[1,2]上的最大值比最小值大 ,求a的值.
,求a的值.
答 案:当a>1时,f(x)=ax为增函数,在[1,2]上,f(x)max=f(2)=a2,f(x)min=f(1)=a,所以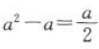 ,即a(2a-3)=0,所以a=0(舍)或
,即a(2a-3)=0,所以a=0(舍)或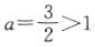 ,所以
,所以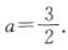 当
当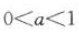 时,f(x)=ax为减函数,同理,在[1,2]上有
时,f(x)=ax为减函数,同理,在[1,2]上有 ,即a(2a-1)=0,所以a=0(舍)或
,即a(2a-1)=0,所以a=0(舍)或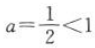 ,故
,故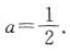
综上所述,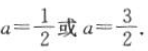
2、解不等式组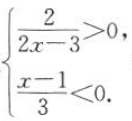 .(解集用区间表示)
.(解集用区间表示)
答 案:由得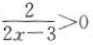 得
得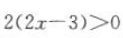 ,解得
,解得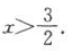 又由
又由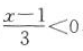 ,解得x<1.
,解得x<1.
所以该不等式组的解集是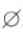 .
.



