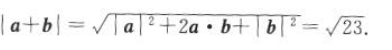2023年高职单招《数学》每日一练试题02月16日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
判断题
1、抛物线y2=-8x的焦点坐标是(2,0).
答 案:错
解 析: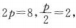 焦点为(一2,0).
焦点为(一2,0).
2、log39=log3(3×3)=3.
答 案:错
解 析:log39=log332=2.
单选题
1、从甲地到乙地一天中有3班长途客运车,有2次列车可到达,从乙地到丙地有2班长途客运车,有3次列车可达,从甲地到丙地一天中有直飞航班2班,则从甲到丙地不同的到达方式有()
答 案:C
解 析:甲→乙→丙:(3+2)X (2+3)=25种方式
甲→丙:2种方式
共27种
2、男女共有8人,从中选男2人和女1人站一排,不同的站法有180种,则其中女的人数为()
答 案:B
解 析: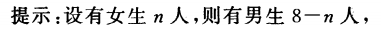
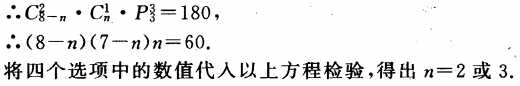
主观题
1、如图,在正三棱柱ABC-A1B1C1中,D为BC的中点,AA1=AB=1.(1)证明:A1C//平面AB1D;
(2)求二面角B-AB1-D的正切值.

答 案:(1)证明:连接A1B,AB1,交于点E,则E是AB1的中点,连接DE,如图所示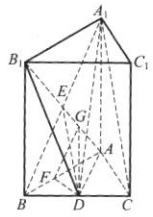 .因为D为BC的中点,所以DE是△A1EC的中位线,DE//A1C.因为A1C
.因为D为BC的中点,所以DE是△A1EC的中位线,DE//A1C.因为A1C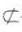 平面AB1D,DE
平面AB1D,DE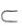 平面AB1D,所以A1C//平面AB1D.(2)过D作DF⊥AB于F,过F作FG⊥AB1于G,连接DG.如上图所示.
平面AB1D,所以A1C//平面AB1D.(2)过D作DF⊥AB于F,过F作FG⊥AB1于G,连接DG.如上图所示.
因为平面A1ABB1⊥平面ABC,DF⊥AB,所以DF⊥平面A1ABB1.
因为AB1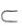 平面A1ABB1,所以AB1⊥DF.
平面A1ABB1,所以AB1⊥DF.
因为FG⊥AB1,所以AB1⊥平面DFG,所以AB1⊥DG.
因为AB1⊥FG,AB1⊥DG,FG∩DG=G,所以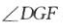 为二面角B-AB1-D的平面角.
为二面角B-AB1-D的平面角.
因为AA1=AB=1,所以在等边三角形ABC中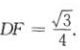
在△ABB1中,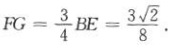
所以在Rt△DFG中,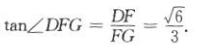
2、用2,3,4三个数字排成一个三位数,求排出的数是偶数的概率.
答 案:根据题意,将2,3,4三个数字排成一个三位数共有六种情况,分别是234,243,324,342,432,423,其中偶数是234,324,342,432,共有四种情况,且这四种情况是等可能的,所以排出的数是偶数的概率为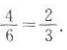
填空题
1、如果在等差数列{an} 中, a3+a4+a5=6,那么a1+a7= ()
答 案:4
解 析:设公差为d,则由a3=a4-d,a5=a4+d,a3+a4+a5=3a4=6 .解得a4=2,根据等差中项的性质,可得a1+a7=2a4=4 .
2、若双曲线经过点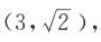 ,且渐近线方程为
,且渐近线方程为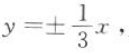 ,则此双曲线的方程为()
,则此双曲线的方程为()
答 案: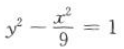
解 析:由双曲线的渐近线方程为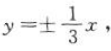 则可设双曲线的标准方程为
则可设双曲线的标准方程为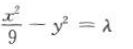
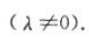 又因为双曲线经过点
又因为双曲线经过点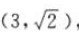 所以
所以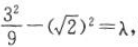 解得
解得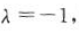 则双曲线的方程
则双曲线的方程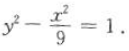
简答题
1、已知函数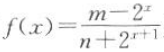 是R上的奇函数.
是R上的奇函数.
(1)求m,n的值;
(2)证明:对于任意的x,恒有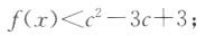
(3)若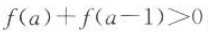 ,求实数a的取值范围.
,求实数a的取值范围.
答 案:(1)因为函数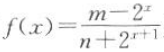 是R上的奇函数,则f(0)=0,所以
是R上的奇函数,则f(0)=0,所以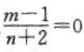 ,所以m=1.因为f(-1)=-f(1),所以
,所以m=1.因为f(-1)=-f(1),所以 ,解得n=2.
,解得n=2.
(2)证明:由(1)知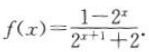 因为
因为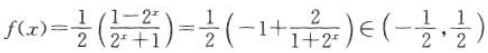 ,而
,而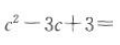
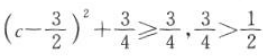 ,所以对于任意的x,恒有
,所以对于任意的x,恒有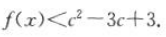
(3) 是减函数.因为
是减函数.因为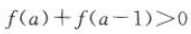 ,f(x)是R上的奇函数,所以
,f(x)是R上的奇函数,所以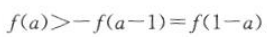 ,所以
,所以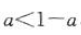 ,所以
,所以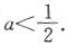 故实数a的取值范围为
故实数a的取值范围为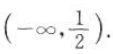
2、已知|a|=2,|b|=5,且a▪b=-3,求|a+b|和|a-b|。
答 案: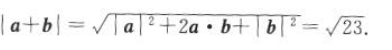

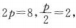 焦点为(一2,0).
焦点为(一2,0).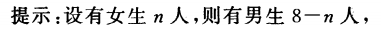

 .因为D为BC的中点,所以DE是△A1EC的中位线,DE//A1C.因为A1C
.因为D为BC的中点,所以DE是△A1EC的中位线,DE//A1C.因为A1C 平面AB1D,DE
平面AB1D,DE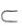 平面AB1D,所以A1C//平面AB1D.(2)过D作DF⊥AB于F,过F作FG⊥AB1于G,连接DG.如上图所示.
平面AB1D,所以A1C//平面AB1D.(2)过D作DF⊥AB于F,过F作FG⊥AB1于G,连接DG.如上图所示.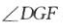 为二面角B-AB1-D的平面角.
为二面角B-AB1-D的平面角.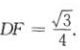
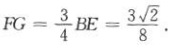
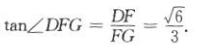
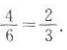
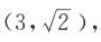 ,且渐近线方程为
,且渐近线方程为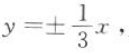 ,则此双曲线的方程为()
,则此双曲线的方程为()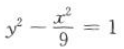
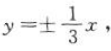 则可设双曲线的标准方程为
则可设双曲线的标准方程为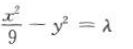
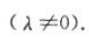 又因为双曲线经过点
又因为双曲线经过点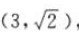 所以
所以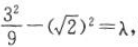 解得
解得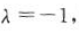 则双曲线的方程
则双曲线的方程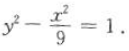
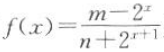 是R上的奇函数.
是R上的奇函数.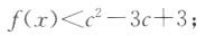
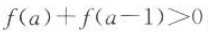 ,求实数a的取值范围.
,求实数a的取值范围.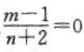 ,所以m=1.因为f(-1)=-f(1),所以
,所以m=1.因为f(-1)=-f(1),所以 ,解得n=2.
,解得n=2.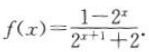 因为
因为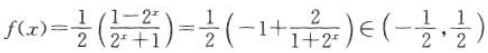 ,而
,而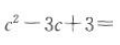
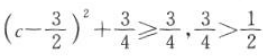 ,所以对于任意的x,恒有
,所以对于任意的x,恒有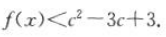
 是减函数.因为
是减函数.因为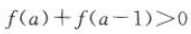 ,f(x)是R上的奇函数,所以
,f(x)是R上的奇函数,所以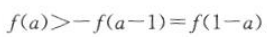 ,所以
,所以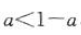 ,所以
,所以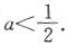 故实数a的取值范围为
故实数a的取值范围为