2023年高职单招《数学》每日一练试题02月15日

2023年高职单招《数学》每日一练试题02月15日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

判断题

1、不等式x²-5x-6≤0的解集是(x|-2≤x≤3}.

答 案：错

解 析：因为x²-5x-6=(x-6)(x+1)≤0,所以-1≤x≤6.

2、同时抛三枚硬币，恰有两枚硬币正面朝上的概率是.

答 案：对

解 析：每一枚硬币有2种情况，三枚硬币就是2³=8种情况，两枚正面朝上即为一枚反面朝上，可能有3种情况，所以概率为

单选题

1、已知|a|=2，|b|=3，且=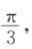向量a,b的内积是().  

• A：
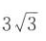
• B：3
• C：
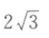
• D：

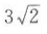
答 案：B

解 析：a▪b=|a||b|cos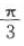=2×3cos=2×3×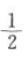=3，故选B。

2、下列命题中属于真命题的是（）  

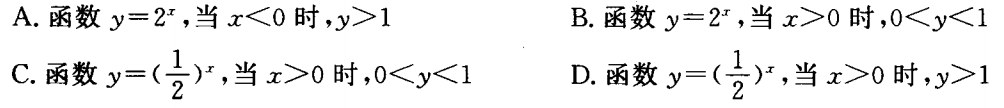
• A：A
• B：B
• C：C
• D：D

答 案：C

主观题

1、已知函数f(x)=log₃(3x—1).(1)求函数f(x)的定义域；
(2)若f(x)<1,求x的取值范围.

答 案：(1)根据题意可得，3x-1>0,解得所以函数f(x)的定义域是(2)因为f(x)=log₃(3x-1)<1=log₃3,f(x)为定义域上的增函数，所以O<3x-1<3,解得所以x的取值范围是

2、某小组有6名男生与4名女生，任选3个人去参观某展览，求：(1)3个人都是男生的概率；
(2)至少有2个男生的概率.

答 案：(1)从6名男生与4名女生中任选3个人，3个人都是男生的概率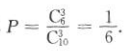(2)从6名男生与4名女生中任选3个人，至少有2个男生的概率

填空题

1、函数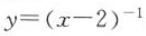的定义域是（）

答 案：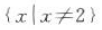

解 析：函数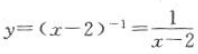,因为分母不为0,所以x-2≠0,即x≠2.

2、设a=(m+1)i-3j,b=i+(m-1)j,其中i,j不共线，(a+b)(a—b),则m=（）  

答 案：-2  

简答题

1、已知向量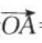=(3,-4),=(6,-3)。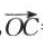=(5-m,-3-m). (1)若A,B,C三点共线，求实数m的值； (2)若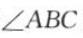为锐角，求实数m的取值范围.

答 案：（1）已知向量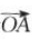=（3，-4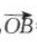），=（6，-3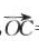），=（5-m，-3-m）。 所以 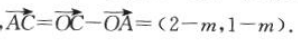因为A,B,C三点共线，所以向量共线，3（1-m）=2-m，解得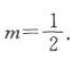 （2）由题可知 因为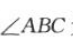为锐角，所以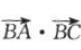=（-3）×（-1-m）+（-1）×（-m）>0,解得 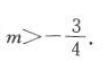又由（1）可知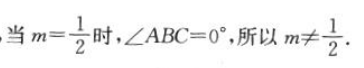， 所以实数m的取值范围为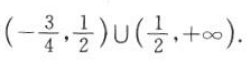

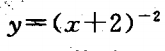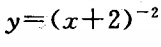2、已知函数： （1）求定义域和值域； （2）讨论函数的单调性； （3）画出函数的图像，观察函数与函数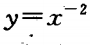的图像的关系。  

答 案：