2023年高职单招《数学》每日一练试题02月12日
2023-02-12 12:39:03 来源:吉格考试网
2023年高职单招《数学》每日一练试题02月12日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
判断题
1、已知函数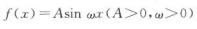 的最大值为2,最小正周期为
的最大值为2,最小正周期为 ,则函数f(x)=2sin4x.
,则函数f(x)=2sin4x.
答 案:对
解 析:因为函数f(x)的最大值是2,所以A=2.又因为最小正周期 ,解得
,解得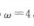 ,所以函数f(x)的解析式为f(x)=2sin4x.
,所以函数f(x)的解析式为f(x)=2sin4x.
2、log39=log3(3×3)=3.
答 案:错
解 析:log39=log332=2.
单选题
1、直线3x+y-5=0与圆x2+y2-10y=0的位置关系是().
- A:相交
- B:相切 n
- C:相离
- D:无法确定
答 案:A
解 析:圆x2+y2-10y=0化成标准方程x2+(y-5)2=25.圆心为(0,5),半径r=5,圆心到直线3x+y-5=0的距离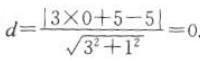 因为d<r,所以直线与圆相交.故选A.
因为d<r,所以直线与圆相交.故选A.
2、—组平行线有5条,与它们都垂直相交的另一组平行线有4条,由这些平行线所围成的长方形的个数是()
- A:12
- B:60
- C:126
- D:240
答 案:B
解 析: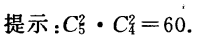
主观题
1、三名运动员练习篮球投篮,每名运动员投进的概率都是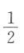 ,求在一次投篮中;(1)三名运动员同时投进的概率;
,求在一次投篮中;(1)三名运动员同时投进的概率;
(2)至少有两名运动员投进的概率.
答 案:(1)三名运动员同时投进的概率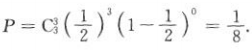 (2)有两名运动员投进的概率
(2)有两名运动员投进的概率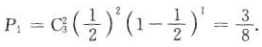
有三名运动员投进的概率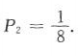
所以至少有两名运动员投进的概率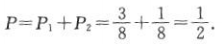
2、如图,设F1,F2分别为椭圆 的左、右焦点,且|F1F2|=2√2.(1)求椭圆C的标准方程;
的左、右焦点,且|F1F2|=2√2.(1)求椭圆C的标准方程;
(2)设P为第一象限内位于椭圆C上的一点,过点P和F2的直线交y轴于点Q.若QF1⊥QF2,求线段PQ的长.
答 案:(1)由题意得F1(-√2,0),F2(V2,0),c=√2,a2=16-a2+c2,解得a2=9.所以椭圆C的标准方程为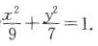 (2)因为QF1与QF2垂直且相等,所以△QF1F2为等腰直角三角形.
(2)因为QF1与QF2垂直且相等,所以△QF1F2为等腰直角三角形.
又|F1F2|=2√2,所以|QF1|=|QF2|=2.
设|PF2|=m,因为|PF1|+|PF2|=2a,所以|PF1|=2×√9-m=6-m.
因为△QPF1为直角三角形,所以|QF1|2+|PQ|2=|PF1|2.
即22+(2+m)2=(6-m)2,m2+4m+8=x2-12m+36,解得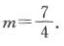 所以
所以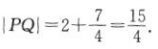
填空题
1、在数列{an}中, a2=2,a17=66,通项公式是项数n的一次式,则 an=______ .
答 案: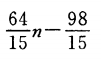
2、若a表示“向东走10km”,b表示“向南走10km”,则a+b表示_____,a-b表示_____
答 案:向东南走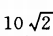 km、向东北走
km、向东北走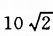 km
km
简答题
1、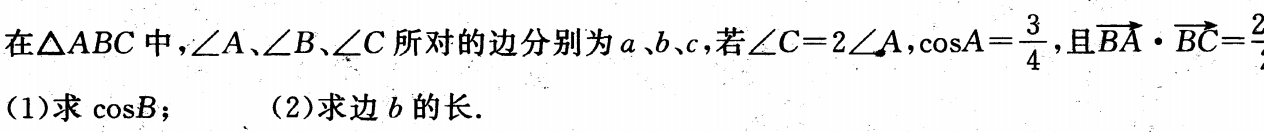
答 案: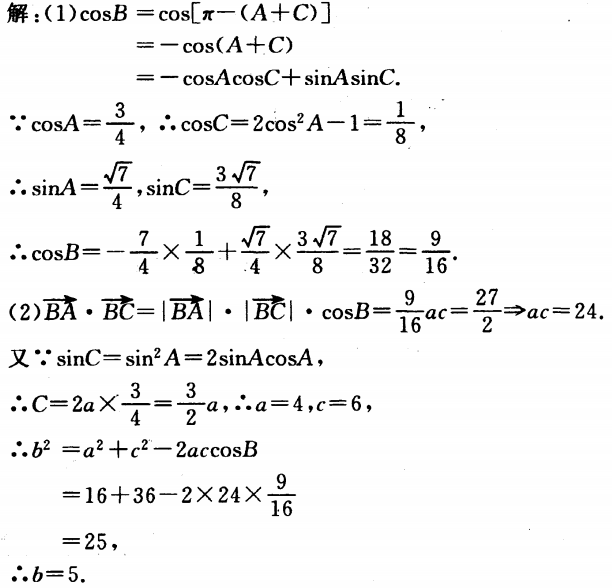
2、已知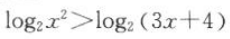 ,求x的取值范围.
,求x的取值范围.
答 案:根据题意可得 解得
解得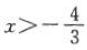 且x≠0.因为
且x≠0.因为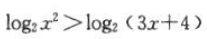 ,所以
,所以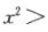
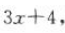 即
即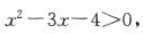 解得
解得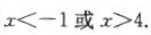 综上所述,x的取值范围是
综上所述,x的取值范围是