2023年高职单招《数学》每日一练试题02月03日
2023-02-03 12:27:48 来源:吉格考试网
2023年高职单招《数学》每日一练试题02月03日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
判断题
1、已知函数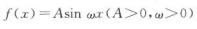 的最大值为2,最小正周期为
的最大值为2,最小正周期为 ,则函数f(x)=2sin4x.
,则函数f(x)=2sin4x.
答 案:对
解 析:因为函数f(x)的最大值是2,所以A=2.又因为最小正周期 ,解得
,解得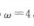 ,所以函数f(x)的解析式为f(x)=2sin4x.
,所以函数f(x)的解析式为f(x)=2sin4x.
2、同时抛三枚硬币,恰有两枚硬币正面朝上的概率是 .
.
答 案:对
解 析:每一枚硬币有2种情况,三枚硬币就是23=8种情况,两枚正面朝上即为一枚反面朝上,可能有3种情况,所以概率为
单选题
1、设a≠0,a∈R,则抛物线y=4ax2的焦点坐标为().
- A:(a,0)
- B:(0,a)
- C:
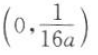
- D:随a符号而定
答 案:C
2、设平面向量a=(2,1),b=(0,-2),则与a+2b垂直的向量可以是().
- A:(4,-6)
- B:(4,6)
- C:(3,-2)
- D:(3.2)
答 案:D
解 析:由题意可知a+2b=(2,-3),4×2+(-6)×(-3)=26,4×2+6×(-3)=-10,3×2+(-2)×(-3)=12,3×2+2×(-3)=0.故选D.
主观题
1、已知函数f(x)=log3(3x—1).(1)求函数f(x)的定义域;
(2)若f(x)<1,求x的取值范围.
答 案:(1)根据题意可得,3x-1>0,解得 所以函数f(x)的定义域是
所以函数f(x)的定义域是 (2)因为f(x)=log3(3x-1)<1=log33,f(x)为定义域上的增函数,所以O<3x-1<3,解得
(2)因为f(x)=log3(3x-1)<1=log33,f(x)为定义域上的增函数,所以O<3x-1<3,解得
 所以x的取值范围是
所以x的取值范围是
2、组委会要从小张、小赵、小李、小罗、小王五名志愿者中选派四人分别从事翻译、导游、礼仪、司机四项不同工作,若其中小张和小赵只能从事前两项工作,其余三人均能从事这四项工作,则不同的选派方案共有多少种?
答 案:分两种情况:(1)小张、小赵去一人:有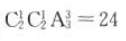 种选派方案;(2)小张、小赵都去:有
种选派方案;(2)小张、小赵都去:有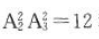 种选派方案.所以共有24+12=36种不同的选派方案.
种选派方案.所以共有24+12=36种不同的选派方案.
填空题
1、若直线x+y+a=0(其中a为常数)经过圆x2+y2-2x+4y-6=0的圆心,则a的值是()
答 案: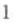
解 析:圆x2+y2-2x+4y-6=0的方程可化为(x-1)2+(y+2)2=11,所以圆心坐标为(1,—2).因为直线x+y+a=0过圆心,所以1-2+a=0,解得a=1.
2、数列9,99,999,9999,....的通项公式为_____。
答 案: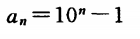
简答题
1、如图所示,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2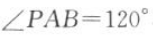 ,
, 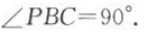 (1)求证:
(1)求证: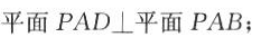 (2)求三棱锥D-PAC的体积.
(2)求三棱锥D-PAC的体积. 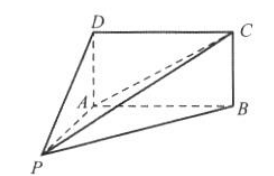
答 案:(1)证明:因为底面ABCD为矩形,所以 因为
因为 且
且 所以
所以 则A
则A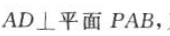 又因为
又因为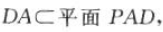 所以平面
所以平面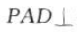 平面PAB.
(2)
平面PAB.
(2)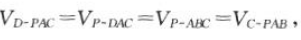 由(1)知
由(1)知 ,所以
,所以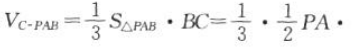
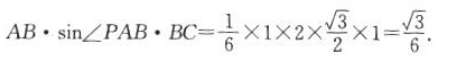
2、如果8个人排成前后两排,每排4人,共有多少种不同的排法?
答 案: