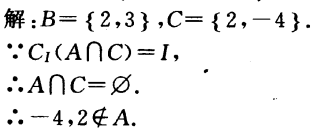2023年高职单招《数学》每日一练试题01月30日
2023-01-30 12:36:03 来源:吉格考试网
2023年高职单招《数学》每日一练试题01月30日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
判断题
1、不等式x2-5x-6≤0的解集是(x|-2≤x≤3}.
答 案:错
解 析:因为x2-5x-6=(x-6)(x+1)≤0,所以-1≤x≤6.
2、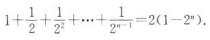
答 案:错
解 析:等比数列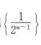 前n项和
前n项和
单选题
1、点P(4,5)关于直线3x-y+3=0的对称点Q的坐标是
- A:(0,13)
- B:(-8,-5)
- C:(-2,7)
- D:(-5,8)
答 案:C
解 析:
2、函数f(x)=cos3xcosx-sin3xsinx的最小正周期为().
- A:

- B:
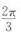
- C:π
- D:2π
答 案:A
解 析:f(x)=cos3rcosx-sin3rsinx=cos4x,其最小正周期
主观题
1、用2,3,4三个数字排成一个三位数,求排出的数是偶数的概率.
答 案:根据题意,将2,3,4三个数字排成一个三位数共有六种情况,分别是234,243,324,342,432,423,其中偶数是234,324,342,432,共有四种情况,且这四种情况是等可能的,所以排出的数是偶数的概率为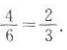
2、如图,在正三棱柱ABC-A1B1C1中,D为BC的中点,AA1=AB=1.(1)证明:A1C//平面AB1D;
(2)求二面角B-AB1-D的正切值.
答 案:(1)证明:连接A1B,AB1,交于点E,则E是AB1的中点,连接DE,如图所示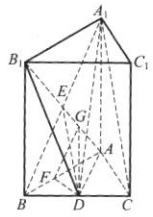 .因为D为BC的中点,所以DE是△A1EC的中位线,DE//A1C.因为A1C
.因为D为BC的中点,所以DE是△A1EC的中位线,DE//A1C.因为A1C 平面AB1D,DE
平面AB1D,DE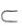 平面AB1D,所以A1C//平面AB1D.(2)过D作DF⊥AB于F,过F作FG⊥AB1于G,连接DG.如上图所示.
平面AB1D,所以A1C//平面AB1D.(2)过D作DF⊥AB于F,过F作FG⊥AB1于G,连接DG.如上图所示.
因为平面A1ABB1⊥平面ABC,DF⊥AB,所以DF⊥平面A1ABB1.
因为AB1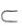 平面A1ABB1,所以AB1⊥DF.
平面A1ABB1,所以AB1⊥DF.
因为FG⊥AB1,所以AB1⊥平面DFG,所以AB1⊥DG.
因为AB1⊥FG,AB1⊥DG,FG∩DG=G,所以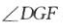 为二面角B-AB1-D的平面角.
为二面角B-AB1-D的平面角.
因为AA1=AB=1,所以在等边三角形ABC中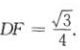
在△ABB1中,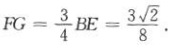
所以在Rt△DFG中,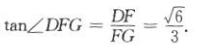
填空题
1、已知α的终边经过点P(3m,-4m),若m>0,则sinα =______,cosα =______,tanα=______.
答 案: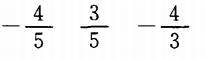
解 析:∵m>0,角α的终边经过点P(3m,-4m),
∴x=3m,y=-4m,r=5m
∴sinα=y/r=-4/5,cosα=x/r=3/5
tanα=sinα/cosα=-4/3
2、函数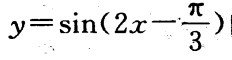 的最小正周期是____,最大值是_____,最小值是_____。
的最小正周期是____,最大值是_____,最小值是_____。
答 案: ,1,-1
,1,-1
简答题
1、已知等差数列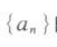 的公差d=2,a1a2a4成等比数列.
的公差d=2,a1a2a4成等比数列.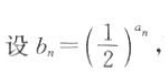 证明:数列{bn}是等比数列
证明:数列{bn}是等比数列
答 案:证明:因为a1,a2,a4成等比数列,所以 即
即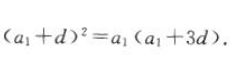 则
则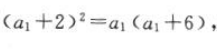 解得a1=2,所以等差数列{an}的通项公式为
解得a1=2,所以等差数列{an}的通项公式为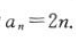 将
将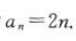 代入bn,
代入bn,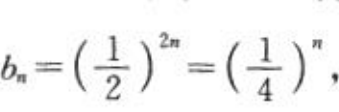 则
则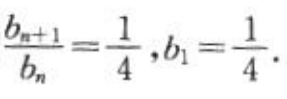 所以{bn}是首项为
所以{bn}是首项为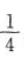 、公比为
、公比为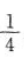 的等比数列。
的等比数列。
2、全集I=R,集合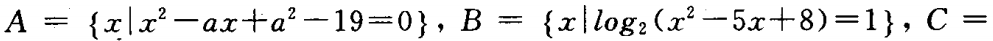
 ,若
,若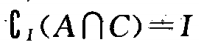 和
和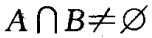 同时成立,求实数a的值。
同时成立,求实数a的值。
答 案: