课程
题库
分享到空间
分享到新浪微博
分享到QQ
分享到微信

2023年高职单招《数学》每日一练试题01月26日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
判断题
1、已知集合A={-1,0,1,2},B={x|x<0},则A∩B={-1,0}.
答 案:错
解 析:A∩B是集合A和集合B中相同元素的集合,即A∩B={-1).
2、log39=log3(3×3)=3.
答 案:错
解 析:log39=log332=2.
单选题
1、取1,2,3,4,5这5个数字中的两个分别作为一个对数的底数和真数,则所得的不同值的个数有()
答 案:B
解 析:1不能作对数的底数,1作真数时无论底数在可取值范围内取几,其值总是0,这就是说,含1的值只有一个0,不含1的,就是2,3,4,5中任选两个做底数与真数,共有值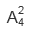 =12,共有不同值1+12=13.
=12,共有不同值1+12=13.
2、若直线3x+4y+k=0与圆x2+y2-6x+5=0相切,则k的值等于()
- A:1或-19
- B:10或-10
- C:-1或-19
- D:-1或19
答 案:A
解 析:提示:配方,(x-3)2+y2=4,因为直线与圆相切,所以 .即|k+9|=10解得k=1或-19
.即|k+9|=10解得k=1或-19
主观题
1、从2,3,4,7,9这五个数字任取3个,组成没有重复数字的三位数,则:(1)这样的三位数一共有多少个?
(2)所有这些三位数的个位上的数字之和是多少?
(3)所有这些三位数的和是多少?
答 案:(1)共有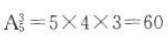 个.(2)因为每个数字会在个位上出现
个.(2)因为每个数字会在个位上出现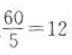 次,5个数字的和是25,所以所求和为25×12=300.(3)由(2)知,个位、十位、百位数字之和均为300,则三位数之和为300×100+300×10+300=33300.
次,5个数字的和是25,所以所求和为25×12=300.(3)由(2)知,个位、十位、百位数字之和均为300,则三位数之和为300×100+300×10+300=33300.
2、三名运动员练习篮球投篮,每名运动员投进的概率都是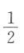 ,求在一次投篮中;(1)三名运动员同时投进的概率;
,求在一次投篮中;(1)三名运动员同时投进的概率;
(2)至少有两名运动员投进的概率.
答 案:(1)三名运动员同时投进的概率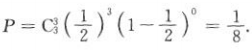 (2)有两名运动员投进的概率
(2)有两名运动员投进的概率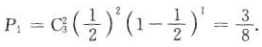
有三名运动员投进的概率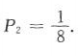
所以至少有两名运动员投进的概率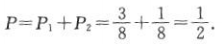
填空题
1、设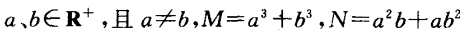 ,则M与N的大小关系是_____.
,则M与N的大小关系是_____.
答 案:M>N
2、已知函数f(x)与g(x)的图像关于y轴对称,且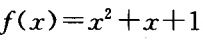 ,则g(x)=______。
,则g(x)=______。
答 案: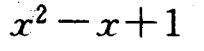
简答题
1、如图所示,正方体ABCD-A1B1C1D1的棱长为1,求三棱锥B-ACB1的体积.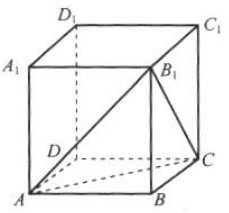
答 案:因为正方体ABCD-A1B1C1D1的棱长为1,所以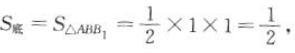 ,h=BC=1.
所以三棱锥B-ACB1的体积为
,h=BC=1.
所以三棱锥B-ACB1的体积为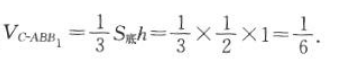
2、求证:函数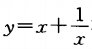 在
在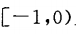 上是减函数。
上是减函数。
答 案: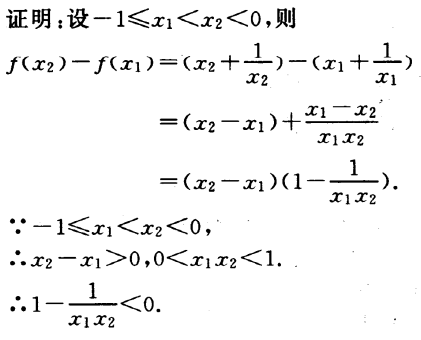
温馨提示:因考试政策、内容不断变化与调整,本站提供的以上信息仅供参考,如有异议,请考生以权威部门公布的内容为准!
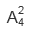 =12,共有不同值1+12=13.
=12,共有不同值1+12=13. .即|k+9|=10解得k=1或-19
.即|k+9|=10解得k=1或-19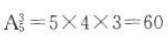 个.(2)因为每个数字会在个位上出现
个.(2)因为每个数字会在个位上出现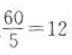 次,5个数字的和是25,所以所求和为25×12=300.(3)由(2)知,个位、十位、百位数字之和均为300,则三位数之和为300×100+300×10+300=33300.
次,5个数字的和是25,所以所求和为25×12=300.(3)由(2)知,个位、十位、百位数字之和均为300,则三位数之和为300×100+300×10+300=33300.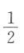 ,求在一次投篮中;(1)三名运动员同时投进的概率;
,求在一次投篮中;(1)三名运动员同时投进的概率;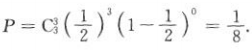 (2)有两名运动员投进的概率
(2)有两名运动员投进的概率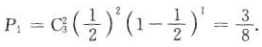
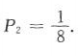
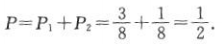
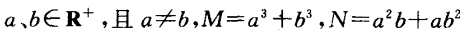 ,则M与N的大小关系是_____.
,则M与N的大小关系是_____. 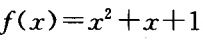 ,则g(x)=______。
,则g(x)=______。
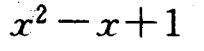

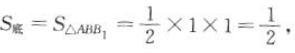 ,h=BC=1.
所以三棱锥B-ACB1的体积为
,h=BC=1.
所以三棱锥B-ACB1的体积为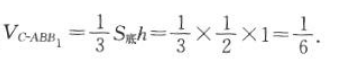
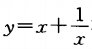 在
在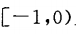 上是减函数。
上是减函数。