2023年高职单招《数学》每日一练试题01月23日

2023年高职单招《数学》每日一练试题01月23日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

判断题

1、同时抛三枚硬币，恰有两枚硬币正面朝上的概率是.

答 案：对

解 析：每一枚硬币有2种情况，三枚硬币就是2³=8种情况，两枚正面朝上即为一枚反面朝上，可能有3种情况，所以概率为

2、已知向量a=(x,-3),b=(3,1),若a⊥b,则x=-9.

答 案：错

解 析：若a⊥b,则a·b=0,即3x-3=0,即x=1.

单选题

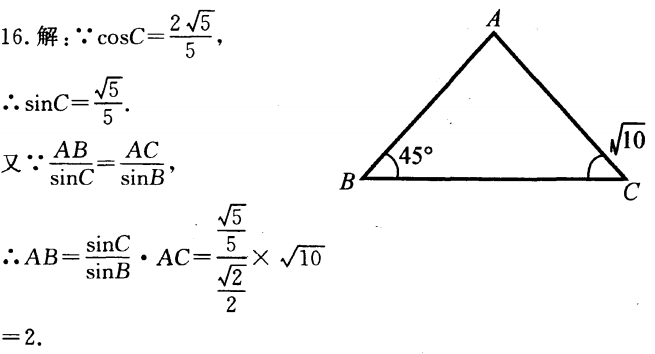
1、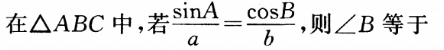  

• A：90°
• B：60°
• C：45°
• D：30°

答 案：C

解 析：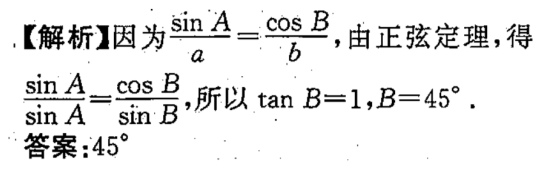

2、已知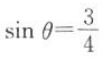,且θ为第二象限角，那么2θ为().

• A：第一象限角
• B：第二象限角
• C：第三象限角
• D：第四象限角

答 案：C

主观题

1、如图，设F₁,F₂分别为椭圆的左、右焦点，且|F₁F₂|=2√2.(1)求椭圆C的标准方程；
(2)设P为第一象限内位于椭圆C上的一点，过点P和F₂的直线交y轴于点Q.若QF₁⊥QF_2，求线段PQ的长.

答 案：(1)由题意得F₁（-√2,0),F₂(V2,0),c=√2,a²=16-a²+c²,解得a²=9.所以椭圆C的标准方程为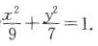(2)因为QF₁与QF₂垂直且相等，所以△QF₁F₂为等腰直角三角形.
又|F₁F₂|=2√2,所以|QF₁|=|QF₂|=2.
设|PF₂|=m,因为|PF₁|+|PF₂|=2a,所以|PF₁|=2×√9-m=6-m.
因为△QPF₁为直角三角形，所以|QF₁|²+|PQ|²=|PF₁|².
即2²+(2+m)²=(6-m)²,m²+4m+8=x²-12m+36,解得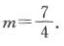所以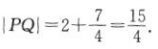

2、如图，在正三棱柱ABC-A₁B₁C₁中，D为BC的中点，AA₁=AB=1.(1)证明：A₁C//平面AB₁D;
(2)求二面角B-AB₁-D的正切值.

答 案：(1)证明：连接A₁B,AB₁,交于点E,则E是AB₁的中点，连接DE,如图所示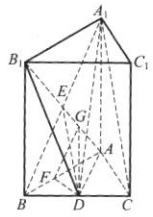.因为D为BC的中点，所以DE是△A₁EC的中位线，DE//A₁C.因为A₁C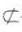平面AB₁D,DE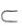平面AB₁D,所以A₁C//平面AB₁D.(2)过D作DF⊥AB于F,过F作FG⊥AB₁于G,连接DG.如上图所示.
因为平面A₁ABB₁⊥平面ABC,DF⊥AB,所以DF⊥平面A₁ABB₁.
因为AB₁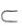平面A₁ABB₁,所以AB₁⊥DF.
因为FG⊥AB₁,所以AB₁⊥平面DFG,所以AB₁⊥DG.
因为AB₁⊥FG,AB₁⊥DG,FG∩DG=G,所以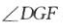为二面角B-AB₁-D的平面角.
因为AA₁=AB=1,所以在等边三角形ABC中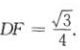
在△ABB₁中，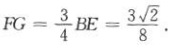
所以在Rt△DFG中，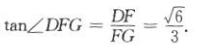

填空题

1、集合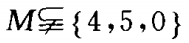，且M中至少有一个偶数，则这样的集合共有_____个。  

答 案：5

解 析：

2、已知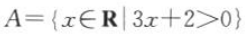集合,集合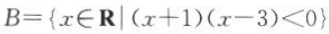,则A∩B=（）.

答 案：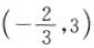

解 析：因为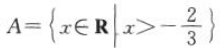集合,集合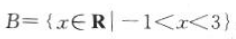,所以A∩B=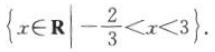

简答题

1、设一直线经过点(-2,4)，它的倾斜角是直线y=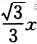+3的倾斜角的2倍，求它的方程.  

答 案：

2、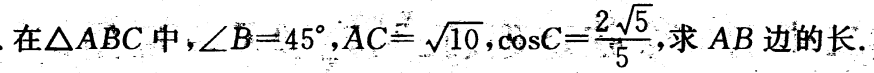  

答 案：