2023年高职单招《数学》每日一练试题01月22日

2023年高职单招《数学》每日一练试题01月22日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

判断题

1、不等式x²-5x-6≤0的解集是(x|-2≤x≤3}.

答 案：错

解 析：因为x²-5x-6=(x-6)(x+1)≤0,所以-1≤x≤6.

2、同时抛三枚硬币，恰有两枚硬币正面朝上的概率是.

答 案：对

解 析：每一枚硬币有2种情况，三枚硬币就是2³=8种情况，两枚正面朝上即为一枚反面朝上，可能有3种情况，所以概率为

单选题

1、函数y=sin 2x的最小正周期是().

• A：
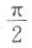
• B：π
• C：2π
• D：4π

答 案：B

解 析：最小正周期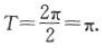故选B.

2、某函数的大致图像如图所示，则该函数可能是().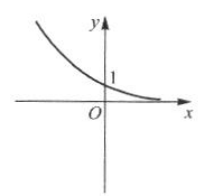

• A：y=2^-x
• B：y=2^x
• C：y=-2^x
• D：y=-2^-x

答 案：A

解 析：因为函数的值域为(0,+∞),所以排除选项C,D.又因为函数为减函数，所以排除选项B.故选A.

主观题

1、已知两直线,当m为何值时，l₁与l₂: (1)相交；(2)平行；(3)重合.  

答 案：(1)当1×3m-(m-2)m²=-m²(m-2)+3m=-m(m-3)(m+1)≠0时，l₁与l₂相交，即m≠0,m≠3且m≠-1. (2)当-m(m-3)(m+1)=0且1×2m-(m-2)×6=12-4m≠0时，l₁与l₂平行，即m=0或m=-1. (3)当-m(m-3)(m+1)=0且12-4m=0时，l₁与l₂重合，即m=3.

2、三名运动员练习篮球投篮，每名运动员投进的概率都是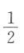,求在一次投篮中；(1)三名运动员同时投进的概率；
(2)至少有两名运动员投进的概率.

答 案：(1)三名运动员同时投进的概率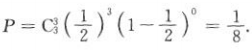(2)有两名运动员投进的概率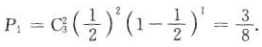
有三名运动员投进的概率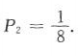
所以至少有两名运动员投进的概率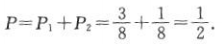

填空题

1、求值：
(1)sin28°cos73°-sin62°cos17°=（）;
(2)cos²75°+cos²15°+cos75°cos15°=（）;
(3)（）.

答 案：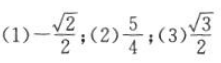

解 析：(1)sin28°cos73°-sin62°cos17°=sin28°cos73°-sin(90°-28°)cos(90°-73°)=sin28°cos73°-cos28°sin73°=sin(28°-73°)=sin(-45°)=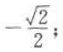(2)原式=sin²15°+cos²15°+sin15°cos15°=
(3)

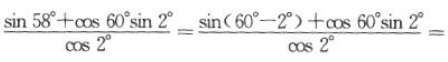
2、已知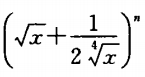：展开式中前3项的系数成等差数列，则展开式中含x的项为_______.

答 案：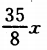

解 析：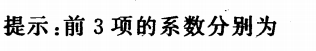

简答题

1、某地兴修水利开一水渠，其断面为等腰梯形，腰与水平线的夹角为60°，要求湿透周长（即断面与水接触的边界长度）为定值L，问渠深h为多少时，可使水流量最大？

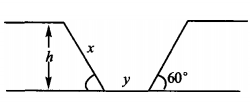
答 案：

2、已知：函数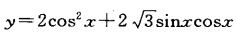，试求函数的单调区间。

答 案：