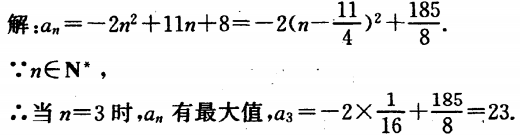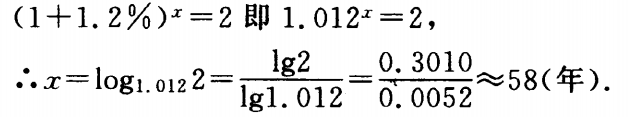2023年高职单招《数学》每日一练试题01月20日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
判断题
1、已知向量a=(x,-3),b=(3,1),若a⊥b,则x=-9.
答 案:错
解 析:若a⊥b,则a·b=0,即3x-3=0,即x=1.
2、不等式x2-5x-6≤0的解集是(x|-2≤x≤3}.
答 案:错
解 析:因为x2-5x-6=(x-6)(x+1)≤0,所以-1≤x≤6.
单选题
1、直线x+ay=2a+2与ax+y=a+1平行(不重合)的充要条件是()
- A:a=1/2
- B:a=-1/2
- C:a=1
- D:a=-1
答 案:C
解 析: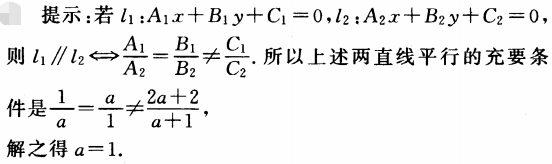
2、偶函数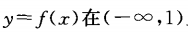 在
在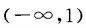 上是增函数,则f(x)在
上是增函数,则f(x)在 上是()
上是()
答 案:B
主观题
1、如图,在正三棱柱ABC-A1B1C1中,D为BC的中点,AA1=AB=1.(1)证明:A1C//平面AB1D;
(2)求二面角B-AB1-D的正切值.

答 案:(1)证明:连接A1B,AB1,交于点E,则E是AB1的中点,连接DE,如图所示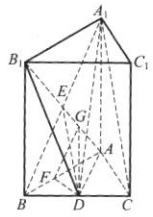 .因为D为BC的中点,所以DE是△A1EC的中位线,DE//A1C.因为A1C
.因为D为BC的中点,所以DE是△A1EC的中位线,DE//A1C.因为A1C 平面AB1D,DE
平面AB1D,DE 平面AB1D,所以A1C//平面AB1D.(2)过D作DF⊥AB于F,过F作FG⊥AB1于G,连接DG.如上图所示.
平面AB1D,所以A1C//平面AB1D.(2)过D作DF⊥AB于F,过F作FG⊥AB1于G,连接DG.如上图所示.
因为平面A1ABB1⊥平面ABC,DF⊥AB,所以DF⊥平面A1ABB1.
因为AB1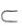 平面A1ABB1,所以AB1⊥DF.
平面A1ABB1,所以AB1⊥DF.
因为FG⊥AB1,所以AB1⊥平面DFG,所以AB1⊥DG.
因为AB1⊥FG,AB1⊥DG,FG∩DG=G,所以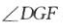 为二面角B-AB1-D的平面角.
为二面角B-AB1-D的平面角.
因为AA1=AB=1,所以在等边三角形ABC中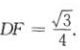
在△ABB1中,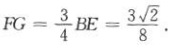
所以在Rt△DFG中,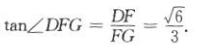
2、三名运动员练习篮球投篮,每名运动员投进的概率都是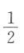 ,求在一次投篮中;(1)三名运动员同时投进的概率;
,求在一次投篮中;(1)三名运动员同时投进的概率;
(2)至少有两名运动员投进的概率.
答 案:(1)三名运动员同时投进的概率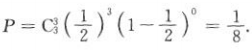 (2)有两名运动员投进的概率
(2)有两名运动员投进的概率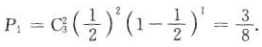
有三名运动员投进的概率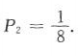
所以至少有两名运动员投进的概率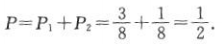
填空题
1、在空间四边形ABCD中,E、F分别是AB、CD的中点,AD丄BC,AD=BC,则EF和BC所成的角是_____.
答 案:45°
解 析: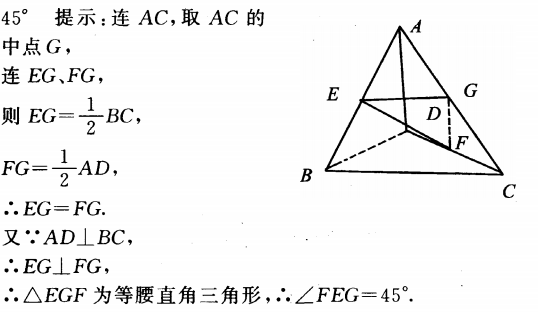
2、甲、乙两射手彼此独立地射击同一目标,甲射中目标的概率为0.8,乙射中目标的概率为0.9,则恰好有一人射中目标的概率为________.
答 案:0.26
解 析:

简答题
1、求由通项公式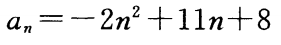 所给定的数列
所给定的数列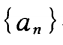 各项中最大项的值。
各项中最大项的值。
答 案: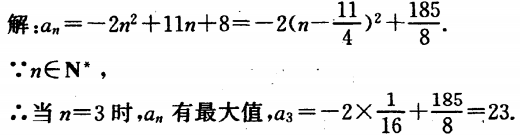
2、某城市的人口年自然增长率为1.2%,求该城市人口的倍增期。
(已知: lg2 =0.3010,lg 1.012=0.0052,lg 1.12=0.0492)
答 案:解:设该城市人口初始量为1,经过x年后,该城市的人口增长两倍,则 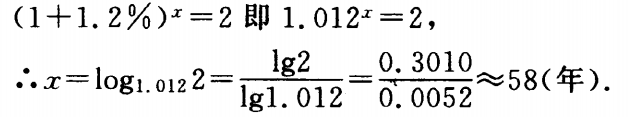
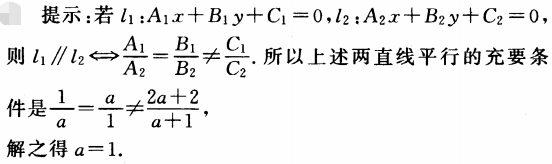
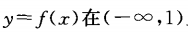 在
在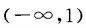 上是增函数,则f(x)在
上是增函数,则f(x)在 上是()
上是()
 .因为D为BC的中点,所以DE是△A1EC的中位线,DE//A1C.因为A1C
.因为D为BC的中点,所以DE是△A1EC的中位线,DE//A1C.因为A1C 平面AB1D,DE
平面AB1D,DE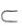 平面AB1D,所以A1C//平面AB1D.(2)过D作DF⊥AB于F,过F作FG⊥AB1于G,连接DG.如上图所示.
平面AB1D,所以A1C//平面AB1D.(2)过D作DF⊥AB于F,过F作FG⊥AB1于G,连接DG.如上图所示.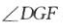 为二面角B-AB1-D的平面角.
为二面角B-AB1-D的平面角.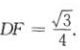
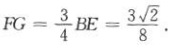
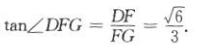
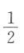 ,求在一次投篮中;(1)三名运动员同时投进的概率;
,求在一次投篮中;(1)三名运动员同时投进的概率;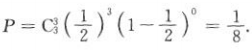 (2)有两名运动员投进的概率
(2)有两名运动员投进的概率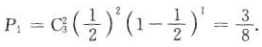
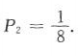
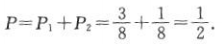


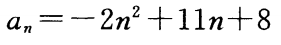 所给定的数列
所给定的数列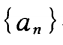 各项中最大项的值。
各项中最大项的值。