2023年高职单招《数学》每日一练试题01月19日
2023-01-19 12:26:55 来源:吉格考试网
2023年高职单招《数学》每日一练试题01月19日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
判断题
1、已知集合A={-1,0,1,2},B={x|x<0},则A∩B={-1,0}.
答 案:错
解 析:A∩B是集合A和集合B中相同元素的集合,即A∩B={-1).
2、设a,b为实数,则“b=3”是“a(b-3)=0”的充分不必要条件.
答 案:对
解 析:当b=3时,a(b-3)=0必定成立,则“b=3”是“a(b-3)=0”的充分条件;当a(b-3)=0时,有可能α=0,b不一定是3,因此“b=3”不是“a(b-3)=0”的必要条件.
单选题
1、不等式x-2<7的解集为().
- A:{x|x≤9}
- B:{x|x≥9}
- C:{x|x<9}
- D:{x|x>9)
答 案:C
解 析:本题考查不等式的解法及用描述法表示解集.
2、已知全集U={1,2,3,4,5,6,7,8,9},A={3,5,7},B={1,3,6,8},那么集合{2,4,9}是().
- A:AUB
- B:A∩B
- C:

- D:
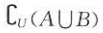
答 案:D
解 析:因为AUB={1,3,5,6,7,8},所以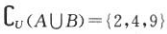 .故选D。
.故选D。
主观题
1、设△ABC的内角A,B,C的对边分别为a,b,c,已知a=2,b=3,c=√5.(1)求sinC的值;
(2)求cos(A+B)+sin2C的值.
答 案:(1)在△ABC中,c2=a2+b2—2abcosC,则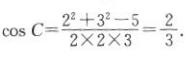 因为o
因为o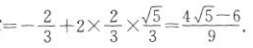
2、如图,设F1,F2分别为椭圆 的左、右焦点,且|F1F2|=2√2.(1)求椭圆C的标准方程;
的左、右焦点,且|F1F2|=2√2.(1)求椭圆C的标准方程;
(2)设P为第一象限内位于椭圆C上的一点,过点P和F2的直线交y轴于点Q.若QF1⊥QF2,求线段PQ的长.
答 案:(1)由题意得F1(-√2,0),F2(V2,0),c=√2,a2=16-a2+c2,解得a2=9.所以椭圆C的标准方程为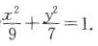 (2)因为QF1与QF2垂直且相等,所以△QF1F2为等腰直角三角形.
(2)因为QF1与QF2垂直且相等,所以△QF1F2为等腰直角三角形.
又|F1F2|=2√2,所以|QF1|=|QF2|=2.
设|PF2|=m,因为|PF1|+|PF2|=2a,所以|PF1|=2×√9-m=6-m.
因为△QPF1为直角三角形,所以|QF1|2+|PQ|2=|PF1|2.
即22+(2+m)2=(6-m)2,m2+4m+8=x2-12m+36,解得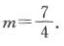 所以
所以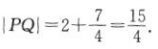
填空题
1、函数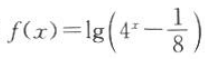 的定义域是().
的定义域是().
答 案: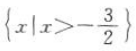
解 析: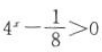 即
即 ,则
,则 ,解得
,解得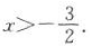
2、数列x,2,y既是等差数列又是等比数列,则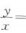 ()
()
答 案:1
解 析:由题意可知,成等差数列可列2-x=y-2,得x+y=4;成等比数列可列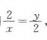 ,得xy=4.联立解得x=2,y=2,所以
,得xy=4.联立解得x=2,y=2,所以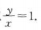
简答题
1、如图所示,三棱锥P-ABC的三条侧棱两两垂直,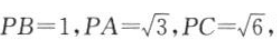 求其体积.
求其体积. 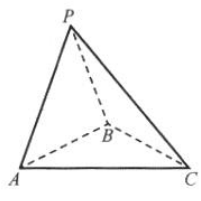
答 案:因为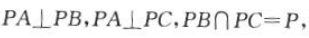 所以
所以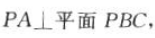 所以PA是三棱锥P-ABC的高.因为
所以PA是三棱锥P-ABC的高.因为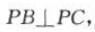 ,所以
,所以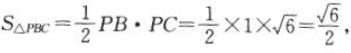 ,所以
,所以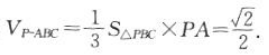
2、已知三个数成等差数列,其和为21,若第二个数减去1,第三个数加上1,则三个数成等比数 列,求原来的三个数.
答 案:设原来的三个数x-d,x,x+d,由其和为21得x=7.又由7-d,6,8+d成等比数列,得 d=4或d=-5,则原来的三个数为3,7,11或12,7,2 .



