2023年高职单招《数学》每日一练试题01月15日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
判断题
1、同时抛三枚硬币,恰有两枚硬币正面朝上的概率是 .
.
答 案:对
解 析:每一枚硬币有2种情况,三枚硬币就是23=8种情况,两枚正面朝上即为一枚反面朝上,可能有3种情况,所以概率为
2、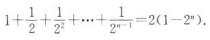
答 案:错
解 析:等比数列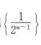 前n项和
前n项和
单选题
1、设直线l经过圆x2+y2+2x+2y=0的圆心,且在y轴上的截距为1,则直线l的斜率为().
- A:2
- B:-2
- C:

- D:
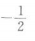
答 案:A
解 析:直线1过圆心(-1,-1)和点(0,1),所以其斜率
2、
答 案:A
主观题
1、拟发行体育奖券,号码从000001到999999,购置时揭号兑奖,若规定从个位数起,第一、三、五位是不同的奇数,第二、四、六位均为偶数时为中奖号码,则中奖率约为多少?(精确到0.1%)
答 案:首先排一、三、五位数字,因为从个位数起,第一、三、五位是不同的奇数,所以从1,3,5,7,9这五个数字中任取三个排列有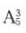 种结果.再因第二、四、六位均为偶数时为中奖号码,先排第二位,从0,2,4,6,8这五个数字中任取一个有
种结果.再因第二、四、六位均为偶数时为中奖号码,先排第二位,从0,2,4,6,8这五个数字中任取一个有 种结果,再排第四位,最后排第六位,同样都有
种结果,再排第四位,最后排第六位,同样都有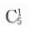 种结果,所以满足条件的中奖号码共有
种结果,所以满足条件的中奖号码共有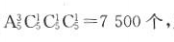 所以中奖率
所以中奖率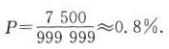
2、已知等差数列{an}的前n项和Sn且S5=35,S8=104.
(1)求数列{an}的通项公式;
(2)若{bn}为等比数列,b1=a2,b2=a3+2,求数列{b,}的公比q及前n项和Tn.
答 案:(1)
 所以a6=19.则数列{an}的公差
所以a6=19.则数列{an}的公差 ,通项公式为an=a6+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以
,通项公式为an=a6+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以 则
则
填空题
1、集合A={x|-1≤x≤3},B={x|x<1},则 =()。
=()。
答 案:[1,3]
解 析:因为集合A={x|-1≤x≤3),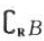 =(x|x≥1),所以
=(x|x≥1),所以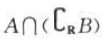 =(x|1≤x≤3).
=(x|1≤x≤3).
2、正四棱锥底面边长为a,侧面积是底面积的2倍,则它的体积是_____.
答 案:
简答题
1、如图所示,过正方形ABCD的顶点A作 设PA=AB=a. (1)求二面角B-PC-D的大小; (2)求平面PAB和平面PCD所成二面角的大小.
设PA=AB=a. (1)求二面角B-PC-D的大小; (2)求平面PAB和平面PCD所成二面角的大小. 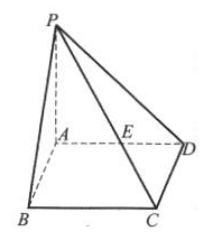
答 案: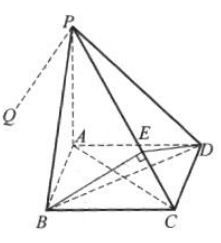 (1)连接AC,BD,如图所示.因为
(1)连接AC,BD,如图所示.因为
 ,所以
,所以 所以
所以 在平面PBC内,作
在平面PBC内,作 ,E为垂足,连接DE,得
,E为垂足,连接DE,得 ,即DE
,即DE PC,即
PC,即 是二面角B-PC-D的平面角.在Rt△PAB中,由PA=AB=a得PB=
是二面角B-PC-D的平面角.在Rt△PAB中,由PA=AB=a得PB= 因为
因为 ,
, 所以
所以 ,所以
,所以 所以PC=
所以PC=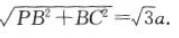 在Rt△PBC中,
在Rt△PBC中,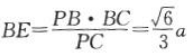 ,同理
,同理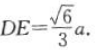 在△BDE中,根据余弦定理,
在△BDE中,根据余弦定理,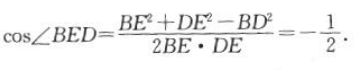 所以
所以 ,此即为二面角B-PC-D的大小.
(2)过P作PQ//AB,则
,此即为二面角B-PC-D的大小.
(2)过P作PQ//AB,则 因为AB//CD,所以PQ//CD.又
因为AB//CD,所以PQ//CD.又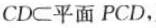 所以平面PAB∩平面PCD=PQ.
因为
所以平面PAB∩平面PCD=PQ.
因为 ,AB//PQ,所以
,AB//PQ,所以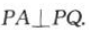 因为
因为 ,
,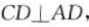 ,所以
,所以 因为PQ//CD,所以
因为PQ//CD,所以 则
则 所以
所以 是平面PAB和平面PCD所成二面角的平面角.
因为PA=AB=AD,所以
是平面PAB和平面PCD所成二面角的平面角.
因为PA=AB=AD,所以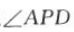 =45°,即平面PAB和PCD所成的二面角是45°.
=45°,即平面PAB和PCD所成的二面角是45°.
2、
答 案:
 .
.
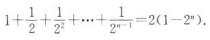
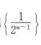 前n项和
前n项和

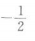


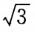
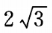
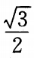
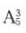 种结果.再因第二、四、六位均为偶数时为中奖号码,先排第二位,从0,2,4,6,8这五个数字中任取一个有
种结果.再因第二、四、六位均为偶数时为中奖号码,先排第二位,从0,2,4,6,8这五个数字中任取一个有 种结果,再排第四位,最后排第六位,同样都有
种结果,再排第四位,最后排第六位,同样都有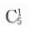 种结果,所以满足条件的中奖号码共有
种结果,所以满足条件的中奖号码共有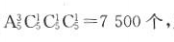 所以中奖率
所以中奖率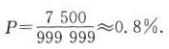

 所以a6=19.则数列{an}的公差
所以a6=19.则数列{an}的公差 ,通项公式为an=a6+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以
,通项公式为an=a6+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以 则
则
 =()。
=()。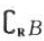 =(x|x≥1),所以
=(x|x≥1),所以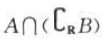 =(x|1≤x≤3).
=(x|1≤x≤3).
 设PA=AB=a. (1)求二面角B-PC-D的大小; (2)求平面PAB和平面PCD所成二面角的大小.
设PA=AB=a. (1)求二面角B-PC-D的大小; (2)求平面PAB和平面PCD所成二面角的大小. 
 (1)连接AC,BD,如图所示.因为
(1)连接AC,BD,如图所示.因为
 ,所以
,所以 所以
所以 在平面PBC内,作
在平面PBC内,作 ,E为垂足,连接DE,得
,E为垂足,连接DE,得 ,即DE
,即DE PC,即
PC,即 是二面角B-PC-D的平面角.在Rt△PAB中,由PA=AB=a得PB=
是二面角B-PC-D的平面角.在Rt△PAB中,由PA=AB=a得PB= 因为
因为 ,
, 所以
所以 ,所以
,所以 所以PC=
所以PC=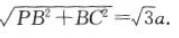 在Rt△PBC中,
在Rt△PBC中,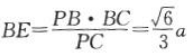 ,同理
,同理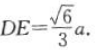 在△BDE中,根据余弦定理,
在△BDE中,根据余弦定理,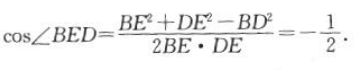 所以
所以 ,此即为二面角B-PC-D的大小.
(2)过P作PQ//AB,则
,此即为二面角B-PC-D的大小.
(2)过P作PQ//AB,则 因为AB//CD,所以PQ//CD.又
因为AB//CD,所以PQ//CD.又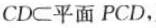 所以平面PAB∩平面PCD=PQ.
因为
所以平面PAB∩平面PCD=PQ.
因为 ,AB//PQ,所以
,AB//PQ,所以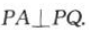 因为
因为 ,
,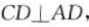 ,所以
,所以 因为PQ//CD,所以
因为PQ//CD,所以 则
则 所以
所以 是平面PAB和平面PCD所成二面角的平面角.
因为PA=AB=AD,所以
是平面PAB和平面PCD所成二面角的平面角.
因为PA=AB=AD,所以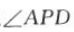 =45°,即平面PAB和PCD所成的二面角是45°.
=45°,即平面PAB和PCD所成的二面角是45°.




