2023年高职单招《数学》每日一练试题01月08日

2023年高职单招《数学》每日一练试题01月08日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

判断题

1、已知向量a=(x,-3),b=(3,1),若a⊥b,则x=-9.

答 案：错

解 析：若a⊥b,则a·b=0,即3x-3=0,即x=1.

2、同时抛三枚硬币，恰有两枚硬币正面朝上的概率是.

答 案：对

解 析：每一枚硬币有2种情况，三枚硬币就是2³=8种情况，两枚正面朝上即为一枚反面朝上，可能有3种情况，所以概率为

单选题

1、若f(x)在[-5，5]上是奇函数，且f(3)＜f(1)，则（）

• A：f(-1)＜f(-3)
• B：f(0)＞f(1)
• C：f(-1)＜f(1)
• D：f(-3)＜f(-5)

答 案：A

解 析：∵f(x)在[-5,5]上是奇函数，
∴f(3)=-f(-3)，f(1)=-f(-1)，
又f(3) < f(1)，则-f(-3) < -f(-1)，
即f(-3) > f(-1)，
故选A．

2、设A、B、C是△ABC的三个内角,且lgsinA=0,sinB和sinC是方程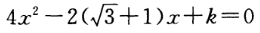的两个根，则k的值为（）  

• A：
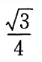
• B：
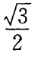
• C：
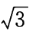
• D：

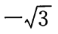
答 案：C

解 析：

主观题

1、设△ABC的内角A,B,C的对边分别为a,b,c,已知a=2,b=3,c=√5.(1)求sinC的值；
(2)求cos(A+B)+sin2C的值.

答 案：(1)在△ABC中，c²=a²+b²—2abcosC,则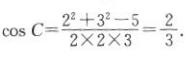因为o(2)在△ABC中，cos(A+B)+sin2C=cos(π-C)+2sinCcosC=-cosC+2sinCcos

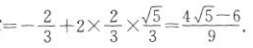
2、已知函数f(x)=log₃(3x—1).(1)求函数f(x)的定义域；
(2)若f(x)<1,求x的取值范围.

答 案：(1)根据题意可得，3x-1>0,解得所以函数f(x)的定义域是(2)因为f(x)=log₃(3x-1)<1=log₃3,f(x)为定义域上的增函数，所以O<3x-1<3,解得所以x的取值范围是

填空题

1、如图，A是∆BCD所在平面外一点，M,N分别是∆ABC和∆ACD的重心，若BD=a，则MN=_______.

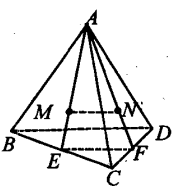
答 案：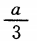

解 析：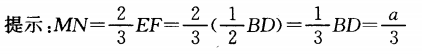

2、椭圆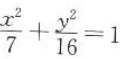上一点M到椭圆的一个焦点的距离是1,则点M到另一个焦点的距离是（）

答 案：7

解 析：由椭圆的方程可知a²=16,b²=7,c²=a²-b²=9,解得c=3,a=4,b=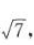|MF₁|+|MF₂|=2a,即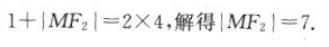

简答题

1、如图，已知扇形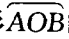的周长是6cm，该扇形的中心角是1弧度，求扇形的面积。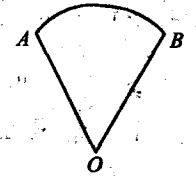  

答 案：  

2、证明：函数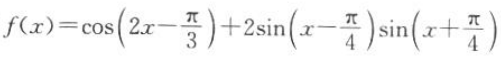的最小正周期是π.

答 案：证明：因为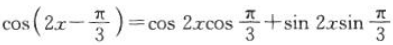


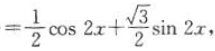
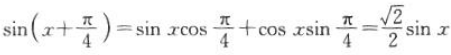
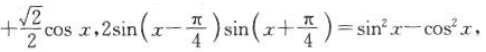
所以
则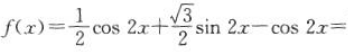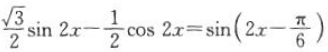的最小正周期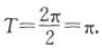
所以函数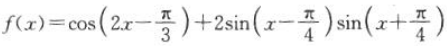的最小正周期是π.