2025年高职单招《数学(中职)》每日一练试题01月06日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、已知向量a=(k-1,3),b=(k,-4),若a⊥b,则k=()
答 案:C
解 析:∵a⊥b,∴a·b=0.又a=(k-1,3),b=(k,-4),∴k(k-1)-12=0,即k2-k-12=0,解得k=-3或k=4.
2、如图所示,直线 ,则直线l的方程是()
,则直线l的方程是()

- A:3x-2y=0
- B:3x+2y-12=0
- C:2x-3y+5=0
- D:2x+3y-13=0
答 案:D
解 析:因为 O(0,0),P(2,3),所以直线 OP的斜率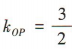 ,又直线
,又直线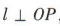 ,所以直线l的斜率
,所以直线l的斜率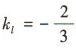 ,因为直线l过点P(2,3),所以直线l的方程为
,因为直线l过点P(2,3),所以直线l的方程为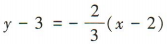 ,即2x+3y-13=0.
,即2x+3y-13=0.
3、在△ABC中,内角A,B,C的对边分别为a,b,c,且△ABC外接圆的半径为1,则a:sinA=()
答 案:B
解 析:
4、已知圆锥的底面半径为 2,高为  ,则其侧面积为()
,则其侧面积为()
- A:
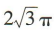
- B:4π
- C:6π
- D:8π
答 案:D
解 析:由圆锥的半径r= 2,高为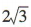 ,可得母线长
,可得母线长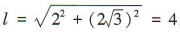 ,所以圆锥的侧面积S=mrl=πx2x4=8π.
,所以圆锥的侧面积S=mrl=πx2x4=8π.
填空题
1、不等式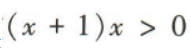 的解集是()
的解集是()
答 案:(-∞,-1)∪(0,+∞)
解 析: 所以原不等式的解集为(-∞,-1)∪(0,+∞)
所以原不等式的解集为(-∞,-1)∪(0,+∞)
2、盒子中有散落的黑白棋子若干粒,已知从中取出2粒都是黑子的概率是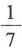 ,从中取出2粒都是白子的概率是
,从中取出2粒都是白子的概率是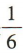 ,则从中任意取出2粒恰好是一粒黑子一粒白子的概率是()
,则从中任意取出2粒恰好是一粒黑子一粒白子的概率是()
答 案: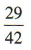
解 析:由题意,任意取出2粒棋子,不考虑先后顺序,一共有2粒都是黑子,2粒都是白子和一粒黑子一粒白子3 种可能.设事件A =“取出2粒都是黑子”,事件B=“取出2粒都是白子”,事件C=“取出2粒恰好是一粒黑子一粒白子”,则A,B,C两两互斥.由已知得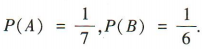 ∵P(AUBUC)= P(A)+ P(B)+ P(C) = 1,∴P(C)=1-P(A)-P(B)=
∵P(AUBUC)= P(A)+ P(B)+ P(C) = 1,∴P(C)=1-P(A)-P(B)=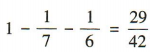 ,∴从中任意取出2粒恰好是一粒黑子一粒白子的概率是
,∴从中任意取出2粒恰好是一粒黑子一粒白子的概率是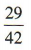
3、在△ABC中,内角A,B,C的对边分别为a,b,c,若a:b:c=3:2:4,则cosC的值为()
答 案:
解 析: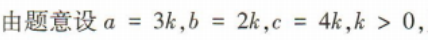
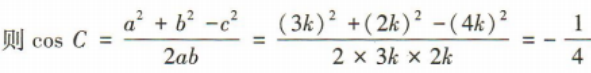
4、若复数(m2-2m)+ mi 是纯虚数,则实数 m 的值为()
答 案:2
解 析:因为复数(m2-2m)+ mi 是纯虚数,所以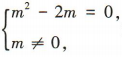 解得 m = 2.
解得 m = 2.
简答题
1、已知函数f(x)=x2+2ax+2,x∈[-5,5].
(1)当a=-1时,求函数f(x)的最大值和最小值;
(2)若f(x)在区间[-5,5]上是单调函数,求实数a的取值范围
答 案:(1)当a=-1时,f(x)=x2-2x+2=(x-1)2+1, 所以在区间[-5,5]上,当x=1时,函数f(x)取得最小值,为f(1)=1,
当x=-5时,函数f(x)取得最大值,为f(-5)=37
(2)f(x)=x2+2ax+2=(x+a)2+2-a2.
若f(x)在区间[-5,5]上是单调函数,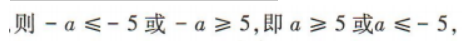 故实数a的取值范围为(-∞,-5]∪[5,+∞).
故实数a的取值范围为(-∞,-5]∪[5,+∞).
2、已知函数f(x)=(x-m)2+2.
(1)若函数f(x)的图像过点(2,2),求函数y=f(x)的单调递增区间;
(2)若函数f(x)是偶函数,求m的值
答 案:(1)由题意知f(2)=(2-m)2+2=2, ∴.m=2,即f(x)=(x-2)2+2,
∴函数f(x)的单调递增区间为[2,+∞).
(2)∵函数f(x)是偶函数,
∴.f(-x)=f(x),即(-x-m)2+2=(x-m)2+2,
∴m=0.
 ,则直线l的方程是()
,则直线l的方程是()

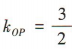 ,又直线
,又直线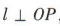 ,所以直线l的斜率
,所以直线l的斜率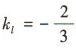 ,因为直线l过点P(2,3),所以直线l的方程为
,因为直线l过点P(2,3),所以直线l的方程为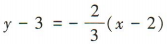 ,即2x+3y-13=0.
,即2x+3y-13=0.
 ,则其侧面积为()
,则其侧面积为()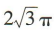
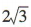 ,可得母线长
,可得母线长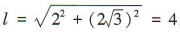 ,所以圆锥的侧面积S=mrl=πx2x4=8π.
,所以圆锥的侧面积S=mrl=πx2x4=8π.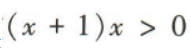 的解集是()
的解集是() 所以原不等式的解集为(-∞,-1)∪(0,+∞)
所以原不等式的解集为(-∞,-1)∪(0,+∞)
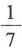 ,从中取出2粒都是白子的概率是
,从中取出2粒都是白子的概率是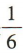 ,则从中任意取出2粒恰好是一粒黑子一粒白子的概率是()
,则从中任意取出2粒恰好是一粒黑子一粒白子的概率是()
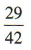
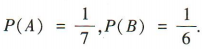 ∵P(AUBUC)= P(A)+ P(B)+ P(C) = 1,∴P(C)=1-P(A)-P(B)=
∵P(AUBUC)= P(A)+ P(B)+ P(C) = 1,∴P(C)=1-P(A)-P(B)=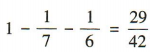 ,∴从中任意取出2粒恰好是一粒黑子一粒白子的概率是
,∴从中任意取出2粒恰好是一粒黑子一粒白子的概率是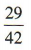

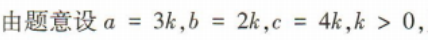
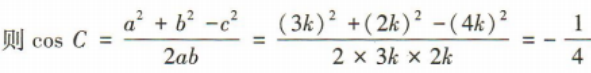
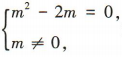 解得 m = 2.
解得 m = 2.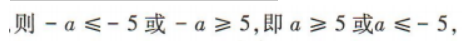 故实数a的取值范围为(-∞,-5]∪[5,+∞).
故实数a的取值范围为(-∞,-5]∪[5,+∞).


