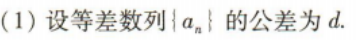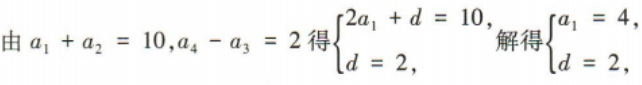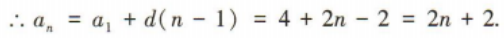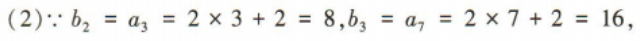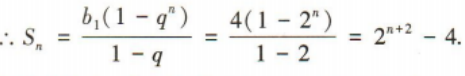2025年高职单招《数学(中职)》每日一练试题01月05日

2025年高职单招《数学(中职)》每日一练试题01月05日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、直线y=2x+1与圆x²+y²-2x+4y=0的位置关系是（）  

• A：相切
• B：相交且过圆心
• C：相离
• D：相交且不过圆心

答 案：A

解 析：由x²+y²-2x+4y=0得(x-1)²+(y+2)²=5,所以该圆的圆心坐标为(1,-2),半径为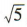,所以圆心(1,-2)到直线y=2x+1,即2x-y+1=0的距离为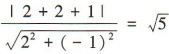,所以直线y=2x+1与圆相切.

2、椭圆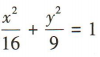的长轴长为()  

• A：1
• B：2
• C：4
• D：8

答 案：D

解 析：由题得a²= 16,解得α= 4(负值舍去),故椭圆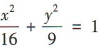的长轴长 2a = 8.

3、掷两颗质地均匀的骰子,朝上的点数相同的概率为（）  

• A：
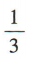
• B：
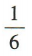
• C：
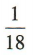
• D：

答 案：B

解 析：掷两颗质地均匀的骰子,所有基本事件共6x6= 36(个).其中点数相同的情况有(1,1),(2,2),(3,3),(4,4),(5,5),(6,6),共6种,所以点数相同的概率为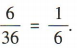

4、如图，在正方体ABCD-A₁B₁C₁D₁中，点E,F分别是棱BB₁,DC的中点，则下列结论错误的是()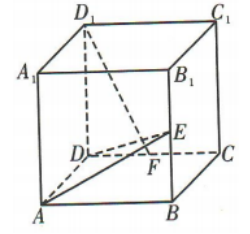

• A：AE⊥D₁F
• B：DE⊥D₁F
• C：AE⊥BC
• D：DE⊥BC

答 案：D

解 析：取CC₁的中点M,连接EM,DM.∵AD⊥平面DD₁C₁C,D₁F⊂平面DD₁C₁C,∴AD⊥D₁F.在正方形DCC₁D₁中，∵F,M分别是DC,C₁C的中点，∴DF=MC.又DD₁=DC,∠D₁DF=∠DCM,:△D₁DF≌△DCM,:∠DD₁F=∠CDM,∴∠CDM+∠D₁FD=∠DD₁F+∠D₁FD=90°,∴D₁F⊥DM.∵DM∩AD=D,DM,AD⊂平面ADME,∴D₁F⊥平面ADME,又AE,DE⊂平面ADME,∴AE⊥D₁F,DE⊥D₁F,故A,B不符合题意.易知BC_⊥平面ABB₁A₁,AE⊂平面ABB₁A₁,∴AE⊥BC,故C不符合题意.易知AD与DE不垂直，BC//AD,∴DE与BC不垂直，故D符合题意.

填空题

1、公比为2的等比数列{an}中，若a₁+a₂=3,则a₄+a₅=（）  

答 案：24

解 析：

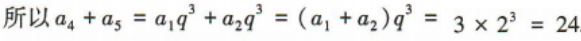
2、已知集合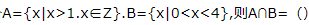

答 案：{2,3}

解 析：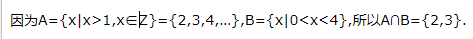

3、设等差数列{a_n}的前n项和为S_n,若S_m-1,=-2,S_m=0,S_m+1=3,则公差d=（）

答 案：1

解 析：因为S_m-1=-2,S_m=0,S_m+1=3,所以a_m=S_m-S_m-1=2,a_m+1=S_m+1-S_m=3,所d=a_m+1-a_m=1.

4、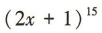的展开式中,含x⁵的项是第()项.  

答 案：11

解 析：易得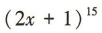的展开式的通项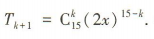令15-k=5,解得k=10,则含x⁵的项是展开式中的第 11 项.

简答题

1、求不等式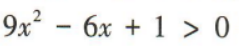的解集.  

答 案：

2、等差数列{an}满足a₁+a₂=10,a₄-a₃=2. (1)求{an}的通项公式； (2)设等比数列{bn}满足b₂=a₃,b₃=a₇,求数列{bn}的前n项和S_n.

答 案：