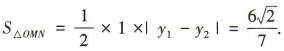2025年高职单招《数学(中职)》每日一练试题01月03日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、从3名男志愿者和2名女志愿者中选2名去支援“冰壶”比赛的相关工作,若冰壶项目需要1男1女两名志愿者,则不同的支援方法的种数是()
答 案:C
解 析:第一步,从3名男志愿者中选1名去支援冰壶项目,有3种选法;第二步,从2名女志愿者中选1名去支援冰壶项目,有2种选法.依据分步乘法计数原理可知,不同的支援方法的种数是3x2=6.
2、先在3张卡片上分别写上3名学生的学号,再把这3张卡片随机分给这3名学生,每人1张,则恰有1名学生分到写自己学号的卡片的概率为()
答 案:D
解 析:设3名学生的学号分别为 1,2,3,则这3名学生分到的卡片情况有(1,2,3),(1,3,2),(2,1,3),(2,3,1),(3,1,2),(3,2,1),共6种,其中恰有1名学生分到写自己学号的卡片的情况有(1,3,2),(2,1,3),(3,2,1),共3种,故恰有1名学生分到写自己学号的卡片的概率为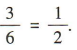
3、若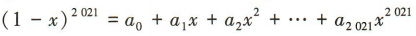 ,则
,则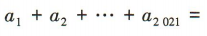
答 案:C
解 析:在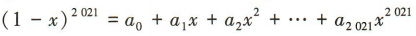 中,令x=0,得a0=1,令x=1,得
中,令x=0,得a0=1,令x=1,得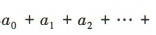
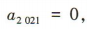 则
则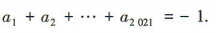
4、已知向量a,b满足la+bl=3,la-bl=2,则a·b=()
答 案:C
解 析:因为|a+b|=3,|a-b|=2,所以|a|2+2a·b+|b|2=9,|a|2-2a·b+|b|²=4,联立得a·b=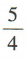 。
。
填空题
1、设等差数列{an}的前n项和为Sn,若Sm-1,=-2,Sm=0,Sm+1=3,则公差d=()
答 案:1
解 析:因为Sm-1=-2,Sm=0,Sm+1=3,所以am=Sm-Sm-1=2,am+1=Sm+1-Sm=3,所d=am+1-am=1.
2、某班有 48 名学生,若任选一人是女生的概率是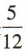 ,则这个班的男生人数是()
,则这个班的男生人数是()
答 案:28
解 析:设这个班的男生人数是x,则这个班的女生人数是48-x. 由题意知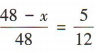 ,解得x=28,所以这个班的男生人数是 28.
,解得x=28,所以这个班的男生人数是 28.
3、(1+x)5的展开式中,二项式系数的和是()
答 案:32
解 析:令x=1,得二项式系数的和为25= 32.
4、抛物线y2=4x的焦点到直线l:5x+12y+3=0的距离是()
答 案: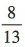
解 析:易知抛物线y2=4x的焦点坐标为(1,0),所以抛物线的焦点到直线l:5x+12y+3=0的距离d=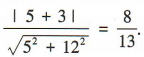
简答题
1、已知i为虚数单位,实数x与y满足(x+y)-xyi=-5+24i,求x与y的值.
答 案:由题意得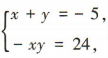 解得
解得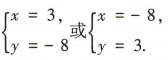
2、已知椭圆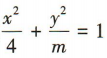 与抛物线y2=4x有共同的焦点F2,过椭圆的左焦点F1作倾斜角为
与抛物线y2=4x有共同的焦点F2,过椭圆的左焦点F1作倾斜角为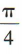 的直线,与椭圆相交于 M,N两点.(1)求直线 MN 的方程和椭圆的方程;
的直线,与椭圆相交于 M,N两点.(1)求直线 MN 的方程和椭圆的方程;
(2)求△OMN的面积(O为坐标原点)
答 案:(1)易得抛物线y2= 4x的焦点为F2(1,0), 所以椭圆的左焦点为F1(-1,0).
又直线 MN 的斜率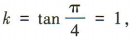 所以直线 MN的方程为y=x+1,即x-y+1=0.
由题意知椭圆焦点在x轴上,且c=1,
所以m=4-1=3,
所以椭圆的方程为
所以直线 MN的方程为y=x+1,即x-y+1=0.
由题意知椭圆焦点在x轴上,且c=1,
所以m=4-1=3,
所以椭圆的方程为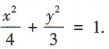 (2)设M,N的坐标分别为(x1,y1),(x2,y2).
由
(2)设M,N的坐标分别为(x1,y1),(x2,y2).
由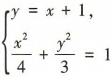 得7x2+8x-8=0,解得
得7x2+8x-8=0,解得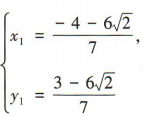 或
或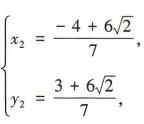 所以 △OMN的面积
所以 △OMN的面积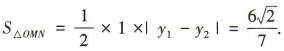



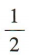
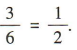
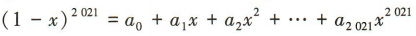 ,则
,则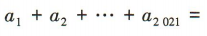
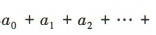
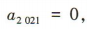 则
则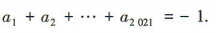
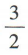
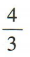
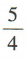
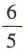
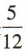 ,则这个班的男生人数是()
,则这个班的男生人数是()
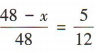 ,解得x=28,所以这个班的男生人数是 28.
,解得x=28,所以这个班的男生人数是 28.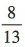
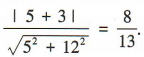
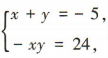 解得
解得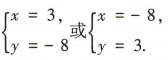
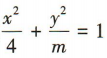 与抛物线y2=4x有共同的焦点F2,过椭圆的左焦点F1作倾斜角为
与抛物线y2=4x有共同的焦点F2,过椭圆的左焦点F1作倾斜角为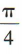 的直线,与椭圆相交于 M,N两点.(1)求直线 MN 的方程和椭圆的方程;
的直线,与椭圆相交于 M,N两点.(1)求直线 MN 的方程和椭圆的方程;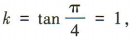 所以直线 MN的方程为y=x+1,即x-y+1=0.
由题意知椭圆焦点在x轴上,且c=1,
所以m=4-1=3,
所以椭圆的方程为
所以直线 MN的方程为y=x+1,即x-y+1=0.
由题意知椭圆焦点在x轴上,且c=1,
所以m=4-1=3,
所以椭圆的方程为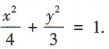 (2)设M,N的坐标分别为(x1,y1),(x2,y2).
由
(2)设M,N的坐标分别为(x1,y1),(x2,y2).
由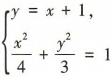 得7x2+8x-8=0,解得
得7x2+8x-8=0,解得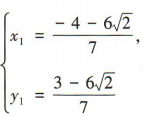 或
或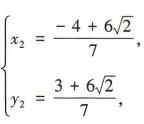 所以 △OMN的面积
所以 △OMN的面积