2025年高职单招《数学(中职)》每日一练试题01月01日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、过点(0,1)且与直线x-y+2=0平行的直线方程为()
- A:x-y+1=0
- B:x-y-1=0
- C:x+y+1=0
- D:x+y-1=0
答 案:A
解 析:易知直线x-y+2=0的斜率为1.因为所求直线与直线x-y+2=0平行,所以所求直线的斜率为1,又所求直线过点(0,1),所以所求直线的方程为y-1=1×(x-0),即x-y+1=0
2、“x=1”是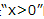 ”的()
”的()
- A:充分条件
- B:必要条件
- C:充要条件
- D:既不充分也不必要条件
答 案:A
解 析:由x=1可推出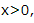 ,故充分性成立,由
,故充分性成立,由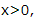 不能推出x=1,故必要性不成立,所以“x=1”是“
不能推出x=1,故必要性不成立,所以“x=1”是“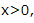 ”的充分不必要条件.
”的充分不必要条件.
3、下列几何体中,为旋转体的是()

答 案:C
解 析:根据旋转体的定义知 ②③ 为旋转体.
4、设奇函数f(x)在[1,4]上为增函数,且最大值为6,那么f(x)在[-4,-1]上为()
- A:增函数,且最小值为-6
- B:增函数,且最大值为6
- C:减函数,且最小值为-6
- D:减函数,且最大值为6
答 案:A
解 析:因为奇函数f(x)在区间[1,4]上为增函数,所以f(x)在区间[-4,-1]上为增函数.易知f(x)在区间[1,4]上的最大值为f(4)=6,f(x)在区间[-4,-1]上的最小值为f(-4).由f(x)为奇函数得f(-4)=-f(4)=-6,故f(x)在区间[-4,-1]上的最小值为-6.
填空题
1、盒子中有散落的黑白棋子若干粒,已知从中取出2粒都是黑子的概率是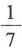 ,从中取出2粒都是白子的概率是
,从中取出2粒都是白子的概率是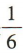 ,则从中任意取出2粒恰好是一粒黑子一粒白子的概率是()
,则从中任意取出2粒恰好是一粒黑子一粒白子的概率是()
答 案: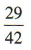
解 析:由题意,任意取出2粒棋子,不考虑先后顺序,一共有2粒都是黑子,2粒都是白子和一粒黑子一粒白子3 种可能.设事件A =“取出2粒都是黑子”,事件B=“取出2粒都是白子”,事件C=“取出2粒恰好是一粒黑子一粒白子”,则A,B,C两两互斥.由已知得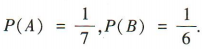 ∵P(AUBUC)= P(A)+ P(B)+ P(C) = 1,∴P(C)=1-P(A)-P(B)=
∵P(AUBUC)= P(A)+ P(B)+ P(C) = 1,∴P(C)=1-P(A)-P(B)=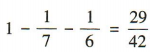 ,∴从中任意取出2粒恰好是一粒黑子一粒白子的概率是
,∴从中任意取出2粒恰好是一粒黑子一粒白子的概率是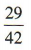
2、在等差数列{an}中,a1=-23,d=2,则数列{an}中负数项的个数为()
答 案:12
解 析:易知an=a1+(n-1)d=-23+(n-1)×2=2n-25.由an=2n-25<0,得n<12.5,所以数列{an}中负数项的个数为12.
3、若双曲线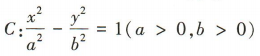 的虚轴长为8,渐近线方程为
的虚轴长为8,渐近线方程为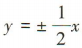 ,则双曲线C的方程为()
,则双曲线C的方程为()
答 案: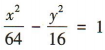
解 析:由题可得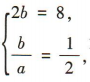 解得
解得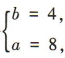 所以双曲线的方程为
所以双曲线的方程为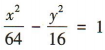
4、某高中学校三个年级共有学生2000名.若在全校学生中随机抽取一名学生,抽到高二年级女生的概率为 0.19,则高二年级的女生人数为()
答 案:380
解 析:易得高二年级的女生人数为2000x0.19=380.
简答题
1、已知 ΔABC的三个顶点分别为A(-3,0),B(2,1),C(-2,3),D为BC 的中点.
(1)求BC边的垂直平分线DE所在直线的方程;
(2)求中线 AD 所在直线的方程.
答 案:(1)因为 B(2,1),C(-2,3), 所以线段 BC的中点D的坐标为(0,2),直线BC的斜率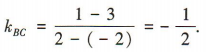 因为 DE是边BC 的垂直平分线,
所以直线 DE的斜率 kDE=2,
所以 DE所在直线的方程为y-2=2(x-0),即2x-y+2=0.
(2)由(1)可得 D(0,2).
因为A(-3,0),
所以直线 AD的方程为
因为 DE是边BC 的垂直平分线,
所以直线 DE的斜率 kDE=2,
所以 DE所在直线的方程为y-2=2(x-0),即2x-y+2=0.
(2)由(1)可得 D(0,2).
因为A(-3,0),
所以直线 AD的方程为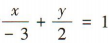 ,即2x-3y+6= 0.
,即2x-3y+6= 0.
2、设甲、乙两人每次射击命中目标的概率分别为 ,且各次射击互相独立.
(1)若甲、乙两人各射击1次,求至少有一人命中目标的概率;
(2)若甲连续射击3次命中目标次数为ξ,求ξ的分布列及数学期望.
,且各次射击互相独立.
(1)若甲、乙两人各射击1次,求至少有一人命中目标的概率;
(2)若甲连续射击3次命中目标次数为ξ,求ξ的分布列及数学期望.
答 案:(1)设“两人都没命中目标”为事件 B,“至少有一人命中目标”为事件 A. 易得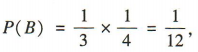 则
则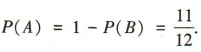 (2)ξ的所有可能取值为0,1,2,3,
则
(2)ξ的所有可能取值为0,1,2,3,
则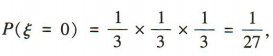
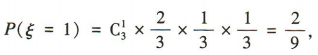
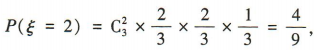
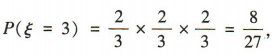 所以ξ的分布列为
所以ξ的分布列为 所以
所以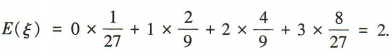
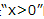 ”的()
”的()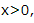 ,故充分性成立,由
,故充分性成立,由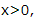 不能推出x=1,故必要性不成立,所以“x=1”是“
不能推出x=1,故必要性不成立,所以“x=1”是“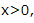 ”的充分不必要条件.
”的充分不必要条件.
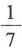 ,从中取出2粒都是白子的概率是
,从中取出2粒都是白子的概率是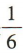 ,则从中任意取出2粒恰好是一粒黑子一粒白子的概率是()
,则从中任意取出2粒恰好是一粒黑子一粒白子的概率是()
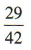
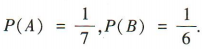 ∵P(AUBUC)= P(A)+ P(B)+ P(C) = 1,∴P(C)=1-P(A)-P(B)=
∵P(AUBUC)= P(A)+ P(B)+ P(C) = 1,∴P(C)=1-P(A)-P(B)=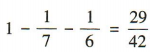 ,∴从中任意取出2粒恰好是一粒黑子一粒白子的概率是
,∴从中任意取出2粒恰好是一粒黑子一粒白子的概率是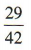
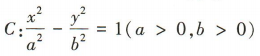 的虚轴长为8,渐近线方程为
的虚轴长为8,渐近线方程为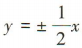 ,则双曲线C的方程为()
,则双曲线C的方程为()
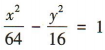
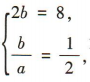 解得
解得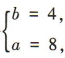 所以双曲线的方程为
所以双曲线的方程为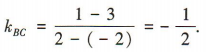 因为 DE是边BC 的垂直平分线,
所以直线 DE的斜率 kDE=2,
所以 DE所在直线的方程为y-2=2(x-0),即2x-y+2=0.
(2)由(1)可得 D(0,2).
因为A(-3,0),
所以直线 AD的方程为
因为 DE是边BC 的垂直平分线,
所以直线 DE的斜率 kDE=2,
所以 DE所在直线的方程为y-2=2(x-0),即2x-y+2=0.
(2)由(1)可得 D(0,2).
因为A(-3,0),
所以直线 AD的方程为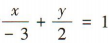 ,即2x-3y+6= 0.
,即2x-3y+6= 0.
 ,且各次射击互相独立.
(1)若甲、乙两人各射击1次,求至少有一人命中目标的概率;
(2)若甲连续射击3次命中目标次数为ξ,求ξ的分布列及数学期望.
,且各次射击互相独立.
(1)若甲、乙两人各射击1次,求至少有一人命中目标的概率;
(2)若甲连续射击3次命中目标次数为ξ,求ξ的分布列及数学期望.
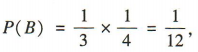 则
则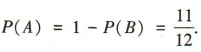 (2)ξ的所有可能取值为0,1,2,3,
则
(2)ξ的所有可能取值为0,1,2,3,
则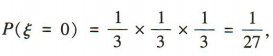
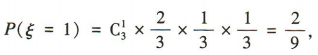
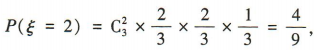
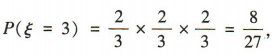 所以ξ的分布列为
所以ξ的分布列为 所以
所以