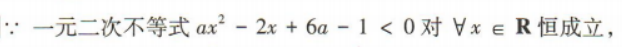2024年高职单招《数学(中职)》每日一练试题12月30日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、已知向量a=(1,2),b=(2,3),c=(-2,2),则(a-b)·c=()
答 案:C
解 析:因为a=(1,2),b=(2,3),所以a-b=(1-2,2-3)=(-1,-1).又c=(-2,2),所以(a-b)·c=-1×(-2)+(-1)×2=0.
2、已知双曲线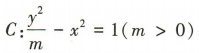 的离心率
的离心率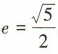 ,则双曲线C的渐近线方程为()
,则双曲线C的渐近线方程为()
答 案:A
解 析:由双曲线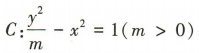 可得 α2= m,b2 =1 因为双曲线C的离心率
可得 α2= m,b2 =1 因为双曲线C的离心率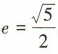 ,所以
,所以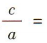
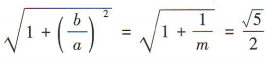 解得m =4,所以a=2,所以双曲线C的渐近线方程为
解得m =4,所以a=2,所以双曲线C的渐近线方程为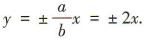
3、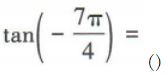
答 案:A
解 析: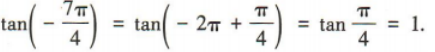
4、不等式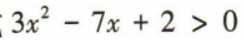 的解集是()
的解集是()
答 案:C
解 析:方程3x2-7x+2=0的两根分别为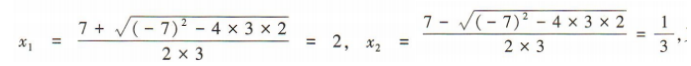

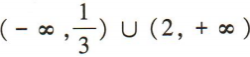
填空题
1、已知sinα=3cosα,那么tan2α的值为()
答 案: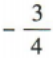
解 析:
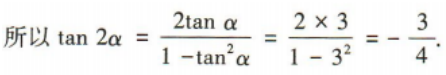
2、已知球的直径为2,则该球的体积是()
答 案: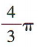
解 析:易得球的半径为1,故球的体积为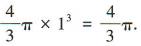
3、如图,在正方体ABCD-A1B1C1D1中,异面直线D1C与BD 所成角的大小为()
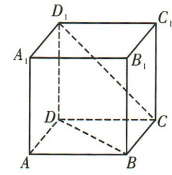
答 案:60°
解 析:在正方体ABCD-A1B1C1D1中,连接B1D1与B1C,如图.易得BD//B1D1,所以 为异面直线D1C与BD所成的角.易知
为异面直线D1C与BD所成的角.易知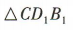 是正三角形,所以
是正三角形,所以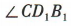 =60°,所以异面直线 D1C与 BD 所成角的大小为 60°.
=60°,所以异面直线 D1C与 BD 所成角的大小为 60°. 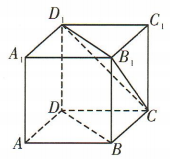
4、在由1,2,3组成的不多于三位的自然数(可以有重复数字)中任意抽取一个,恰好抽中两位自然数的概率是()
答 案: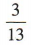
解 析:由1,2,3组成的一位自然数有3个,两位自然数有32= 9(个),三位自然数有33= 27(个),故恰好抽中两位自然数的概率是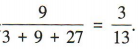
简答题
1、已知焦点在y轴上的抛物线过 P(2,2).(1)求抛物线的标准方程;
(2)已知直线l:y=x+b(b≠0)与抛物线交于点 A,B,若以 AB 为直径的圆过原点O,求直线l的方程.
答 案:(1)设抛物线的方程为 x2= 2py,
因为抛物线过 P(2,2),
所以4=4p,解得p=1,
所以抛物线的标准方程为x2= 2y.
(2)设A(x1,y1),B(x2,y2).
由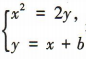 得x2-2x-2b=0,
所以
得x2-2x-2b=0,
所以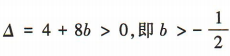 ,x1+x2= 2,x1x2 =-2b.
因为以 AB 为直径的圆过原点O,
所以
,x1+x2= 2,x1x2 =-2b.
因为以 AB 为直径的圆过原点O,
所以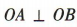 ,则
,则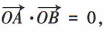 所以x1x2+y1y2 = 0,
所以x1x2+(x1+b)(x2+b)=2x1xz2+b(x1+x2)+b2=0,
所以-2b+b2=0,解得b=2(b=0舍去),符合题意.
所以直线l的方程为y=x+2.
所以x1x2+y1y2 = 0,
所以x1x2+(x1+b)(x2+b)=2x1xz2+b(x1+x2)+b2=0,
所以-2b+b2=0,解得b=2(b=0舍去),符合题意.
所以直线l的方程为y=x+2.
2、若一元二次不等式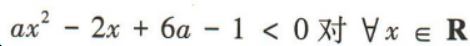 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
答 案: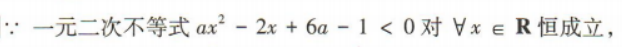

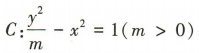 的离心率
的离心率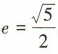 ,则双曲线C的渐近线方程为()
,则双曲线C的渐近线方程为()
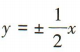
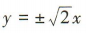
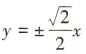
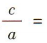
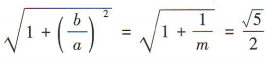 解得m =4,所以a=2,所以双曲线C的渐近线方程为
解得m =4,所以a=2,所以双曲线C的渐近线方程为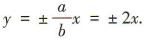
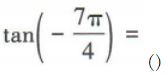
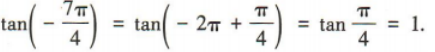
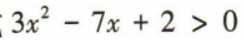 的解集是()
的解集是()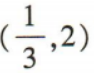
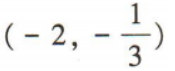
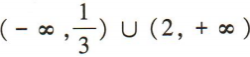

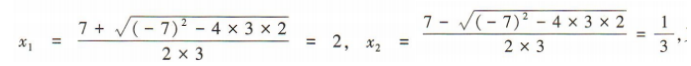

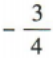

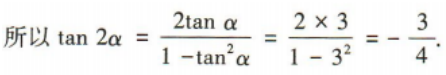
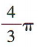
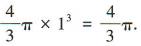

 为异面直线D1C与BD所成的角.易知
为异面直线D1C与BD所成的角.易知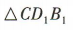 是正三角形,所以
是正三角形,所以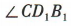 =60°,所以异面直线 D1C与 BD 所成角的大小为 60°.
=60°,所以异面直线 D1C与 BD 所成角的大小为 60°. 
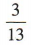
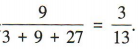
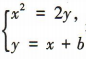 得x2-2x-2b=0,
所以
得x2-2x-2b=0,
所以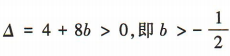 ,x1+x2= 2,x1x2 =-2b.
因为以 AB 为直径的圆过原点O,
所以
,x1+x2= 2,x1x2 =-2b.
因为以 AB 为直径的圆过原点O,
所以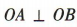 ,则
,则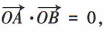 所以x1x2+y1y2 = 0,
所以x1x2+(x1+b)(x2+b)=2x1xz2+b(x1+x2)+b2=0,
所以-2b+b2=0,解得b=2(b=0舍去),符合题意.
所以直线l的方程为y=x+2.
所以x1x2+y1y2 = 0,
所以x1x2+(x1+b)(x2+b)=2x1xz2+b(x1+x2)+b2=0,
所以-2b+b2=0,解得b=2(b=0舍去),符合题意.
所以直线l的方程为y=x+2.
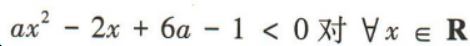 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.