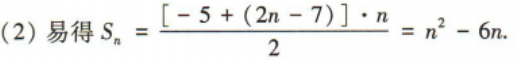2024年高职单招《数学(中职)》每日一练试题12月25日

2024年高职单招《数学(中职)》每日一练试题12月25日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、sin240°的值是()  

• A：
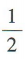
• B：
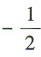
• C：
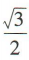
• D：

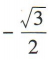
答 案：D

解 析：

2、袋中共有6个除了颜色外完全相同的球,其中有2个黄球和4个白球,从袋中任取一球,该球为黄色的概率是（）  

• A：
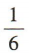
• B：
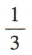
• C：
• D：

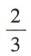
答 案：B

解 析：该球为黄色的概率为

3、“ab=0”是“a=0”的（）  

• A：必要不充分条件
• B：充分不必要条件
• C：充要条件
• D：既不充分又不必要条件

答 案：A

解 析：若a=0,则ab=0;若ab=0,则a不一定等于0.故“ab=0”是“a=0”的必要不充分条件

4、在四边形ABCD中，=（）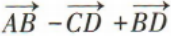

• A：
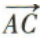
• B：
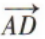
• C：
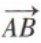
• D：

答 案：A

解 析：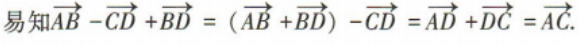

填空题

1、已知数据 10,x,11,y,12,z的平均数为8,则数据 x,y,z的平均数为()  

答 案：5

解 析：易得10+x+y+11+12+z= 48,则x+y+z= 15,故x,y,z的平均数为5.

2、已知扇形的面积为4,圆心角为2rad,则该扇形的周长为（）  

答 案：8

解 析：扇形的半径为r.由扇形的面积为4,圆心角α=2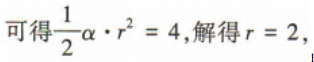 所以扇形的弧长l=α·r=4,所以扇形的周长为l+2r=8.

3、已知函数y=x²-4x+3在区间[-1,m]上有最小值-1.则实数m的取值范围是（）

答 案：[2,+∞)

解 析：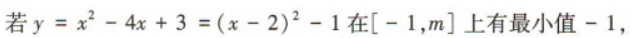

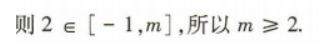
4、已知函数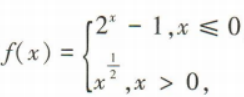若f(m)=3,则m=（）

答 案：9

解 析：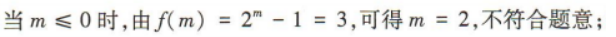

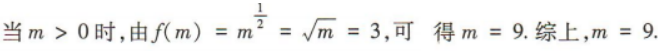
简答题

1、已知焦点在y轴上的抛物线过 P(2,2).(1)求抛物线的标准方程;
(2)已知直线l:y=x+b(b≠0)与抛物线交于点 A,B,若以 AB 为直径的圆过原点O,求直线l的方程.  

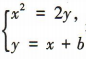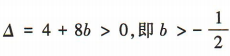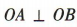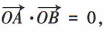答 案：(1)设抛物线的方程为 x²= 2py， 因为抛物线过 P(2,2)， 所以4=4p,解得p=1， 所以抛物线的标准方程为x²= 2y. (2)设A(x₁,y₁),B(x₂,y₂). 由得x²-2x-2b=0, 所以,x₁+x₂= 2,x₁x₂ =-2b. 因为以 AB 为直径的圆过原点O, 所以,则 所以x₁x₂+y₁y₂ = 0, 所以x₁x₂+(x₁+b)(x₂+b)=2x₁xz₂+b(x₁+x₂)+b²=0, 所以-2b+b²=0,解得b=2(b=0舍去),符合题意. 所以直线l的方程为y=x+2.  

2、已知S,是等差数列{an}的前n项和，a1=-5,a3+a4=0. (1)求数列{an}的通项公式； (2)若S_m=40,求m的值.

答 案：