2024年高职单招《数学(中职)》每日一练试题12月24日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、已知集合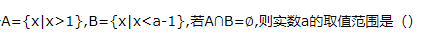
答 案:B
解 析: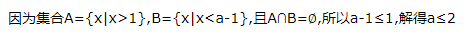
2、已知直线x-y+1=0,圆(x-1)²+y²=2,则直线与圆的位置关系是()
答 案:C
解 析:易知圆(x-1)²+y²=2的半径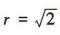 ,圆心坐标为(1,0).因为圆心(1,0)到直线x-y+1=0的距离d=
,圆心坐标为(1,0).因为圆心(1,0)到直线x-y+1=0的距离d=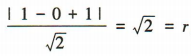 ,所以直线与圆相切.
,所以直线与圆相切.
3、某社区计划在端午节前夕按如下规则设计香囊:在基础配方以外,从佩兰、冰片、丁香、石菖蒲这四味中药中选择两味添加到香囊,则不同的添加方案有()
答 案:C
解 析:从佩兰、冰片、丁香、石菖蒲这四味中药中选两味,有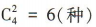 不同的添加方案.
不同的添加方案.
4、已知椭圆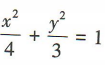 的两个焦点为F1,F2,过F2的直线交椭圆于M,N两点,则△F1MN的周长为()
的两个焦点为F1,F2,过F2的直线交椭圆于M,N两点,则△F1MN的周长为()
答 案:D
解 析:易知椭圆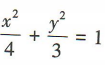 的长半轴长a=2.又M,N是椭圆上的点,F1,F2是椭圆的焦点,所以
的长半轴长a=2.又M,N是椭圆上的点,F1,F2是椭圆的焦点,所以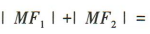
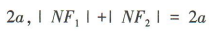 ,所以△F1MN的周长为
,所以△F1MN的周长为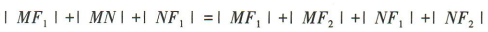 =2a+2a=4a=8。
=2a+2a=4a=8。
填空题
1、若 则sin2α=()
则sin2α=()
答 案: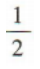
解 析: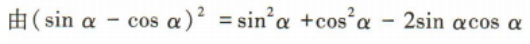
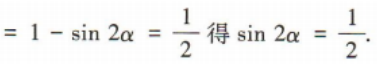
2、已知α是第二象限角,若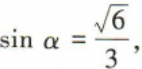 tanα=()
tanα=()
答 案: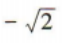
解 析:
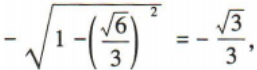
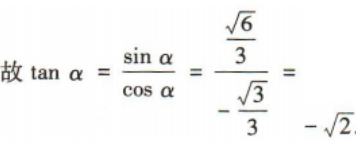
3、将2.5.11三个数分别加上相同的常数m.使得到的三个数依次成等比数列,则m=()
答 案:1
解 析:2+m,5+m,11+m三个数依次成等比数列,所以(5+m)2=(2+m)(11+m),解得m=1.
4、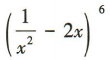 的展开式中各项系数之和为()
的展开式中各项系数之和为()
答 案:1
解 析:令x=1,得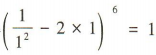 ,即
,即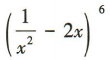 的展开式中各项系数之和为1.
的展开式中各项系数之和为1.
简答题
1、从含有2件次品的10件产品中随机抽取3件产品.求:(1)至多有1件次品的概率;
(2)至少有1件次品的概率.
答 案:从 10 件产品中任取3件,共有 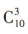 种取法,
(1)设A=“至多有一件次品”.由题意得从含有2件次品的 10件产品中随机抽取3件产品,至多有一件次品有
种取法,
(1)设A=“至多有一件次品”.由题意得从含有2件次品的 10件产品中随机抽取3件产品,至多有一件次品有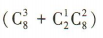 种取法,
所以
种取法,
所以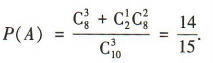 (2)设 B=“至少有一件次品”.由题意得从含有2件次品的 10件产品中随机抽取3件产品,至少有一件次品有
(2)设 B=“至少有一件次品”.由题意得从含有2件次品的 10件产品中随机抽取3件产品,至少有一件次品有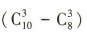 种取法,
所以
种取法,
所以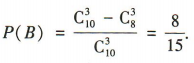
2、某商场想设计一幅周长为12米的矩形电子宣传屏,电子宣传屏设计费为每平方米3000元.设矩形一边长为x米,面积为S平方米.
(1)求出S与x之间的函数关系式,并确定自变量x的取值范围;
(2)请你设计一个方案,使设计商能获得最多的设计费,并求出这个费用.
答 案:(1)∵矩形的周长为12米,一边长为x米, ∴矩形相邻的边长为(6-x)米,∴面积S=x(6-x)=-x2+6x.
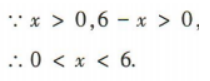
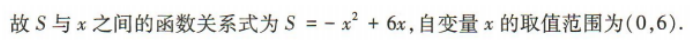
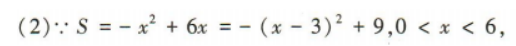 ∴x=3时,S取得最大值,为9,
∴当矩形的长为3米,宽为3米时,矩形的面积最大,为9平方米,此时设计商能获得最多的设计费,为9×3000=27000(元).
∴x=3时,S取得最大值,为9,
∴当矩形的长为3米,宽为3米时,矩形的面积最大,为9平方米,此时设计商能获得最多的设计费,为9×3000=27000(元).
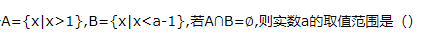
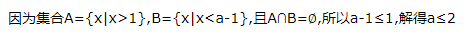
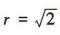 ,圆心坐标为(1,0).因为圆心(1,0)到直线x-y+1=0的距离d=
,圆心坐标为(1,0).因为圆心(1,0)到直线x-y+1=0的距离d=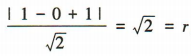 ,所以直线与圆相切.
,所以直线与圆相切.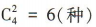 不同的添加方案.
不同的添加方案.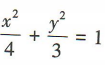 的两个焦点为F1,F2,过F2的直线交椭圆于M,N两点,则△F1MN的周长为()
的两个焦点为F1,F2,过F2的直线交椭圆于M,N两点,则△F1MN的周长为()
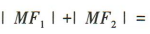
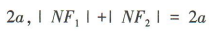 ,所以△F1MN的周长为
,所以△F1MN的周长为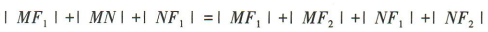 =2a+2a=4a=8。
=2a+2a=4a=8。 则sin2α=()
则sin2α=()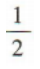
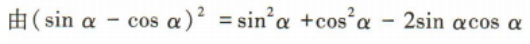
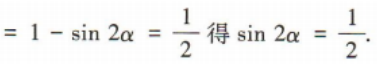
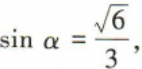 tanα=()
tanα=()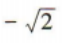

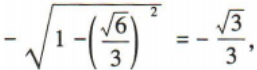
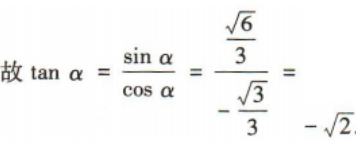
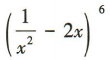 的展开式中各项系数之和为()
的展开式中各项系数之和为()
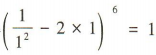 ,即
,即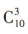 种取法,
(1)设A=“至多有一件次品”.由题意得从含有2件次品的 10件产品中随机抽取3件产品,至多有一件次品有
种取法,
(1)设A=“至多有一件次品”.由题意得从含有2件次品的 10件产品中随机抽取3件产品,至多有一件次品有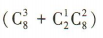 种取法,
所以
种取法,
所以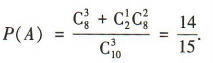 (2)设 B=“至少有一件次品”.由题意得从含有2件次品的 10件产品中随机抽取3件产品,至少有一件次品有
(2)设 B=“至少有一件次品”.由题意得从含有2件次品的 10件产品中随机抽取3件产品,至少有一件次品有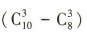 种取法,
所以
种取法,
所以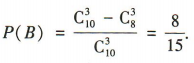
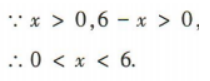
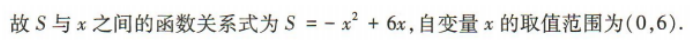
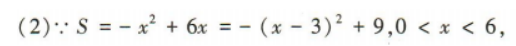 ∴x=3时,S取得最大值,为9,
∴当矩形的长为3米,宽为3米时,矩形的面积最大,为9平方米,此时设计商能获得最多的设计费,为9×3000=27000(元).
∴x=3时,S取得最大值,为9,
∴当矩形的长为3米,宽为3米时,矩形的面积最大,为9平方米,此时设计商能获得最多的设计费,为9×3000=27000(元).


