2024年高职单招《数学(中职)》每日一练试题12月17日

2024年高职单招《数学(中职)》每日一练试题12月17日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、-530°是()  

• A：第一象限角
• B：第二象限角
• C：第三象限角
• D：第四象限角

答 案：C

解 析：-530°=-360°×2+190°,即-530°角的终边与190°角的终边相同.因为190°是第三象限角，所以-530°是第三象限角.

2、在等差数列{an}中，a4+a8=26,则数列{an}的前11项和S11=（）

• A：58
• B：88
• C：143

答 案：C

解 析：因为{a_n}是等差数列，所以a₄+a₈=2a₆=26,解得a₆=13,所以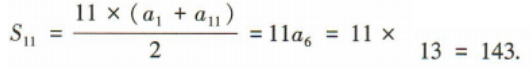

3、已知三点A(1,2),B(-1,3)和C(x-1,5),若共线，则x=（）

• A：-4
• B：-1
• C：1
• D：4

答 案：A

解 析：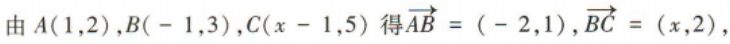

4、已知集合P={-1,0,1,3,4,6},Q={-2,-1,4,5},则PnQ=（）  

• A：{-2,0}
• B：{-1,3}
• C：{0,3,6}
• D：{-1,4}

答 案：D

解 析：由P={-1,0,1,3,4,6},Q={-2,-1,4,5},得P∩Q={-1,4}.

填空题

1、若A是△ABC的一个内角，且（）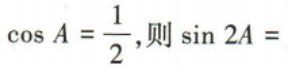

答 案：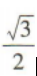

解 析：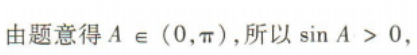

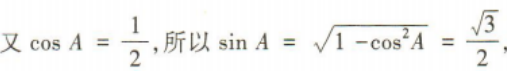
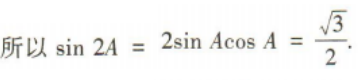
2、盒子中有散落的黑白棋子若干粒,已知从中取出2粒都是黑子的概率是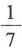,从中取出2粒都是白子的概率是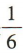,则从中任意取出2粒恰好是一粒黑子一粒白子的概率是（）  

答 案：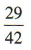

解 析：由题意,任意取出2粒棋子,不考虑先后顺序,一共有2粒都是黑子,2粒都是白子和一粒黑子一粒白子3 种可能.设事件A =“取出2粒都是黑子”,事件B=“取出2粒都是白子”,事件C=“取出2粒恰好是一粒黑子一粒白子”,则A,B,C两两互斥.由已知得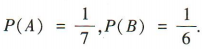∵P(AUBUC)= P(A)+ P(B)+ P(C) = 1,∴P(C)=1-P(A)-P(B)=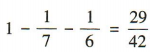，∴从中任意取出2粒恰好是一粒黑子一粒白子的概率是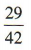

3、已知|a|=|b|=1,a与b的夹角为60°,则(a-2b)·a=（）  

答 案：0

解 析：因为|a|=|b|=1,a与b的夹角为60°,所以(a-2b)·a=a²-2a·b=|a|²-2|a|·|b|·cos60°=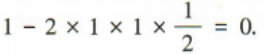

4、已知等差数列{a_n}的前n项和为S_n,且a₁=16,a₂=13,则S₇=（）

答 案：49

解 析：设等差数列{a_n}的公差为d.因为a₁=16,a₂=13,所以d=a₂-a₁=-3,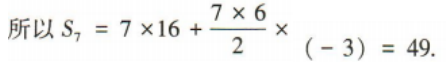

简答题

1、已知函数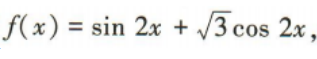x∈R. (1)求函数f(x)的最小正周期； (2)求函数f(x)在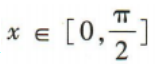上的最值.

答 案：

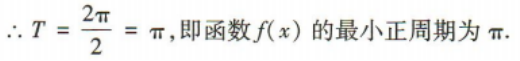
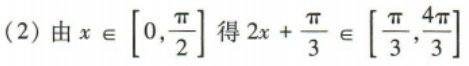
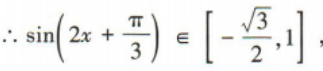
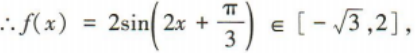
2、已知曲线C的方程为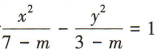,求满足下列条件时,实数m的取值范围,(1)曲线C是椭圆;
(2)曲线C是双曲线.  

答 案：(1)∵曲线C的方程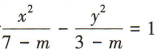可化为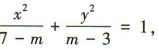 又曲线C是椭圆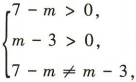， ∴解得30,解得m<3或m>7, 故实数 m 的取值范围为(-∞,3)U(7,+∞).