2024年高职单招《数学(中职)》每日一练试题12月13日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、已知tanα=2,则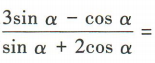 ()
()
答 案:A
解 析:由tanα=2,得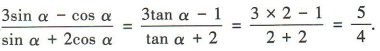
2、已知x∈[0,π],则满足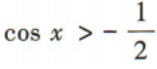 的x的取值范围是()
的x的取值范围是()
答 案:D
解 析: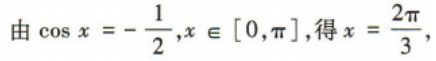


3、下列函数中,为偶函数的是()
- A:y=sinx
- B:y=cosx
- C:y=sinx+cosx
- D:y=sinxcosx
答 案:B
解 析:函数f1(x)=sinx的定义域为R,f1(-x)=sin(-x)=-sinx≠f1(x),所以函数y=sinx不是偶函数;函数f2(x)=cosx的定义域为R,f2(-x)=cos(-x)=cosx=f2(x),所以函数y=cosx是偶函数;函数f3(x)=sinx+cosx的定义域为R,f3(-x)=sin(-x)+cos(-x)=-sinx+cosx≠f3(x),所以函数y=sinx+cosx不是偶函数;函数f₄(x)=sinxcosx的定义域为R,f4(-x)=sin(-x)cos(-x)=-sinxcosx≠f4(x),所以函数y=sinxcosx不是偶函数.
4、命题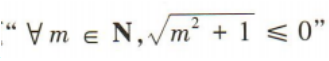 的否定是()
的否定是()
答 案:B
解 析:因为命题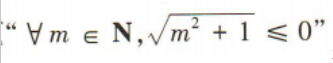 是全称命题,所以其否定是特称命题,即
是全称命题,所以其否定是特称命题,即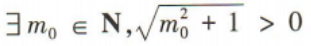
填空题
1、已知α是第二象限角,若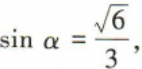 tanα=()
tanα=()
答 案: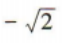
解 析:
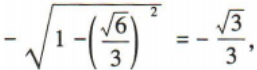
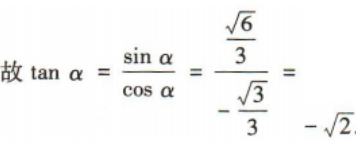
2、函数f(x)=3-2cos4x的最大值为()
答 案:5
解 析: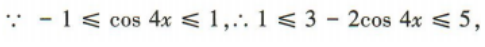 所以最大值是5
所以最大值是5
3、设△ABC的内角A,B,C的对边分别为a,b,c,4a=3b,B=2A,则cosA=()
答 案: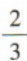
解 析: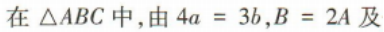
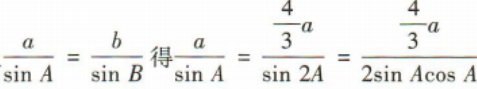

4、已知奇函数f(x)在[-3,0]上单调递减,且f(-3)=2,则f(x)在[0,3]上的最小值为()
答 案:-2
解 析:因为f(x)为奇函数,且在[-3,0]上单调递减,所以f(x)在[0,3]上单调递减,所以f(x)在[0,3]上的最小值为f(3).由f(x)是奇函数,f(-3)=2得f(3)=-f(-3)=-2,所以f(x)在[0,3]上的最小值为-2
简答题
1、已知直线l:x-2y-6=0.(1)若直线l1过点M(1,-2),且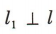 ,求直线l1的方程;
(2)若直线l2//l,且直线l2与直线l之间的距离为
,求直线l1的方程;
(2)若直线l2//l,且直线l2与直线l之间的距离为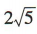 ,求直线l2的方程.
,求直线l2的方程.
答 案:(1)易得直线l的斜率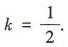 因为
因为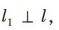 所以直线l1的斜率为-2.
又直线l1过点 M(1,-2),
所以直线l1的方程是y+2=-2(x-1),即2x+y=0.
(2)依题意可设直线l2:x-2y+c=0.
因为直线l2与直线l之间的距离为
所以直线l1的斜率为-2.
又直线l1过点 M(1,-2),
所以直线l1的方程是y+2=-2(x-1),即2x+y=0.
(2)依题意可设直线l2:x-2y+c=0.
因为直线l2与直线l之间的距离为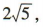 所以
所以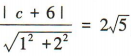 ,解得c=4或c=-16,
所以直线l2的方程是x-2y+4=0或x-2y-16=0.
,解得c=4或c=-16,
所以直线l2的方程是x-2y+4=0或x-2y-16=0.
2、已知△ABC的内角A,B,C的对边分别为a,b,c,且a+b=11,c=7, (1)求a的值;
(2)求sinA和△ABC的面积.
(1)求a的值;
(2)求sinA和△ABC的面积.
答 案:




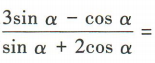 ()
()
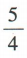
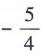
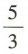
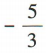
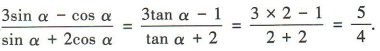
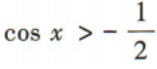 的x的取值范围是()
的x的取值范围是()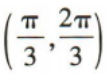
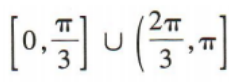
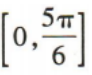
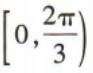
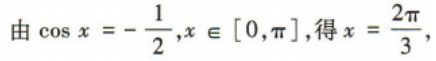


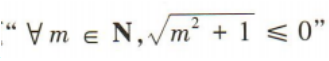 的否定是()
的否定是()
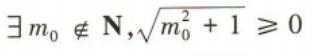
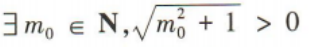
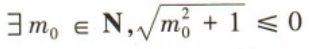
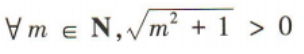
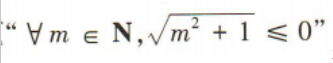 是全称命题,所以其否定是特称命题,即
是全称命题,所以其否定是特称命题,即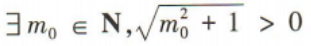
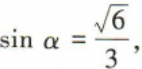 tanα=()
tanα=()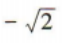

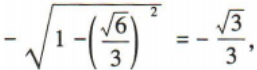
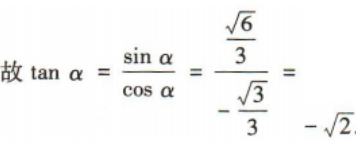
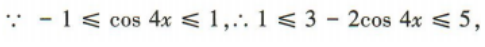 所以最大值是5
所以最大值是5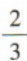
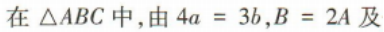
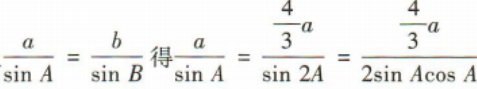

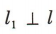 ,求直线l1的方程;
(2)若直线l2//l,且直线l2与直线l之间的距离为
,求直线l1的方程;
(2)若直线l2//l,且直线l2与直线l之间的距离为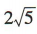 ,求直线l2的方程.
,求直线l2的方程.
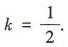 因为
因为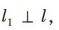 所以直线l1的斜率为-2.
又直线l1过点 M(1,-2),
所以直线l1的方程是y+2=-2(x-1),即2x+y=0.
(2)依题意可设直线l2:x-2y+c=0.
因为直线l2与直线l之间的距离为
所以直线l1的斜率为-2.
又直线l1过点 M(1,-2),
所以直线l1的方程是y+2=-2(x-1),即2x+y=0.
(2)依题意可设直线l2:x-2y+c=0.
因为直线l2与直线l之间的距离为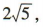 所以
所以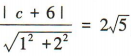 ,解得c=4或c=-16,
所以直线l2的方程是x-2y+4=0或x-2y-16=0.
,解得c=4或c=-16,
所以直线l2的方程是x-2y+4=0或x-2y-16=0.
 (1)求a的值;
(2)求sinA和△ABC的面积.
(1)求a的值;
(2)求sinA和△ABC的面积.







