2024年高职单招《数学(中职)》每日一练试题12月09日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、已知函数f(x)=x3+x,若f(a)=2,则f(-a)的值是()
答 案:A
解 析:f(-a)=(-a)3+(-a)=-a3-a=-(a3+a)=-f(a)=-2.
2、抛物线y²=4x的准线方程为()
答 案:B
解 析:由抛物线y²=4x可知2p=4,则p=2,所以抛物线的准线方程为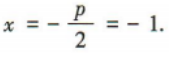
3、下列函数中,最小正周期为π的偶函数是()
答 案:A
解 析:易知y=|sinx|是最小正周期为π的偶函数,y=sin2x是最小正周期为π的奇函数,y=sin|x|不是周期函数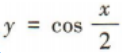 是最小正周期为4π的偶函数.
是最小正周期为4π的偶函数.
4、若奇函数f(x)在[1,3]上是增函数,且最小值是1,则f(x)在[-3,-1]上是()
- A:增函数,最小值是-1
- B:增函数,最大值是-1
- C:减函数,最小值是-1
- D:减函数,最大值是-1
答 案:B
解 析:因为函数f(x)是奇函数,且在[1,3]上是增函数,所以函数f(x)在x=1处取得最小值,所以f(1)=1,所以函数f(x)在[-3,-1]上是增函数,在x=-1处取得最大值.由奇函数的性质得f(-1)=-f(1)=-1,所以f(x)在[-3,-1]上的最大值为-1.
填空题
1、在由1,2,3组成的不多于三位的自然数(可以有重复数字)中任意抽取一个,恰好抽中两位自然数的概率是()
答 案: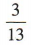
解 析:由1,2,3组成的一位自然数有3个,两位自然数有32= 9(个),三位自然数有33= 27(个),故恰好抽中两位自然数的概率是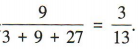
2、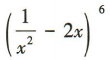 的展开式中各项系数之和为()
的展开式中各项系数之和为()
答 案:1
解 析:令x=1,得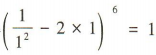 ,即
,即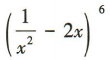 的展开式中各项系数之和为1.
的展开式中各项系数之和为1.
3、已知0是正方形ABCD的中心,则向量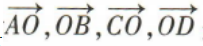 是().(填序号)
①平行向量;②相等向量;③有相同终点的向量;④模都相等的向量
是().(填序号)
①平行向量;②相等向量;③有相同终点的向量;④模都相等的向量
答 案:④
解 析:根据向量的有关概念及正方形的性质,可得向量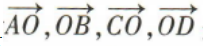 是模都相等的向量
是模都相等的向量
4、已知等差数列{an}的公差为d(d≠0),且a1,a3,a6成等比数列,则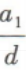 ()
()
答 案:4
解 析: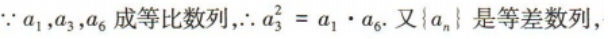
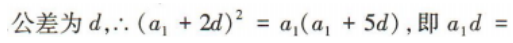
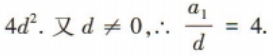
简答题
1、解方程:x2-x+1=0.
答 案:由x2-x+1=0得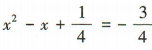 ,即
,即

 ∴方程x2-x+1=0的两根分别为
∴方程x2-x+1=0的两根分别为
2、如图, ,四边形 ABCD是矩形,E,F分别是CD,PB的中点,PD=8,BC=5.
,四边形 ABCD是矩形,E,F分别是CD,PB的中点,PD=8,BC=5.
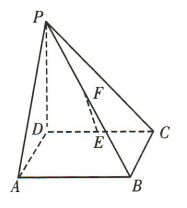 (1)证明EF//平面PAD:
(1)证明EF//平面PAD:
(2)求点P到 AB 的距离.
答 案: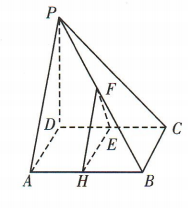 (1)如图,取 AB 的中点 H,连接 EH,FH.
因为 H,F分别是 AB,PB的中点,
所以 FH // PA.
又
(1)如图,取 AB 的中点 H,连接 EH,FH.
因为 H,F分别是 AB,PB的中点,
所以 FH // PA.
又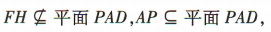 所以 FH //平面 PAD.
因为 H,E分别是 AB,CD 的中点,四边形 ABCD 为矩形,
所以 HE//AD,
又
所以 FH //平面 PAD.
因为 H,E分别是 AB,CD 的中点,四边形 ABCD 为矩形,
所以 HE//AD,
又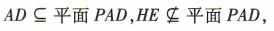 所以EH//平面 PAD.
又
所以EH//平面 PAD.
又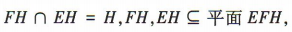 所以平面 FHE//平面PAD.
又
所以平面 FHE//平面PAD.
又 所以EF//平面 PAD.
(2)因为
所以EF//平面 PAD.
(2)因为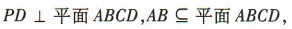 所以
所以  又四边形 ABCD 为矩形,
所以
又四边形 ABCD 为矩形,
所以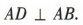 又
又 所以
所以 因为
因为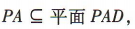 所以
所以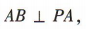 所以 PA 的长为点 P到 AB 的距离,
在
所以 PA 的长为点 P到 AB 的距离,
在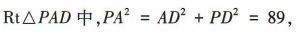 所以
所以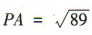 ,即点P到AB 的距离为
,即点P到AB 的距离为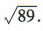
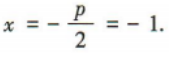



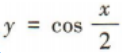 是最小正周期为4π的偶函数.
是最小正周期为4π的偶函数.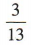
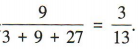
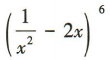 的展开式中各项系数之和为()
的展开式中各项系数之和为()
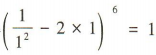 ,即
,即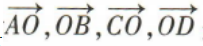 是().(填序号)
①平行向量;②相等向量;③有相同终点的向量;④模都相等的向量
是().(填序号)
①平行向量;②相等向量;③有相同终点的向量;④模都相等的向量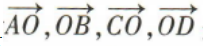 是模都相等的向量
是模都相等的向量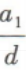 ()
()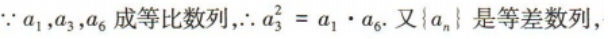
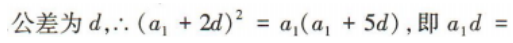
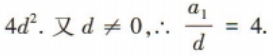
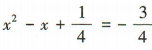 ,即
,即

 ∴方程x2-x+1=0的两根分别为
∴方程x2-x+1=0的两根分别为
 ,四边形 ABCD是矩形,E,F分别是CD,PB的中点,PD=8,BC=5.
,四边形 ABCD是矩形,E,F分别是CD,PB的中点,PD=8,BC=5.
 (1)证明EF//平面PAD:
(1)证明EF//平面PAD: (1)如图,取 AB 的中点 H,连接 EH,FH.
因为 H,F分别是 AB,PB的中点,
所以 FH // PA.
又
(1)如图,取 AB 的中点 H,连接 EH,FH.
因为 H,F分别是 AB,PB的中点,
所以 FH // PA.
又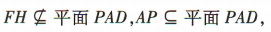 所以 FH //平面 PAD.
因为 H,E分别是 AB,CD 的中点,四边形 ABCD 为矩形,
所以 HE//AD,
又
所以 FH //平面 PAD.
因为 H,E分别是 AB,CD 的中点,四边形 ABCD 为矩形,
所以 HE//AD,
又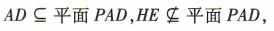 所以EH//平面 PAD.
又
所以EH//平面 PAD.
又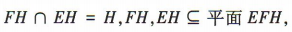 所以平面 FHE//平面PAD.
又
所以平面 FHE//平面PAD.
又 所以EF//平面 PAD.
(2)因为
所以EF//平面 PAD.
(2)因为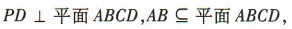 所以
所以  又四边形 ABCD 为矩形,
所以
又四边形 ABCD 为矩形,
所以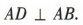 又
又 所以
所以 因为
因为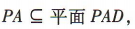 所以
所以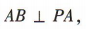 所以 PA 的长为点 P到 AB 的距离,
在
所以 PA 的长为点 P到 AB 的距离,
在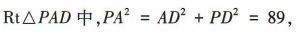 所以
所以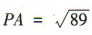 ,即点P到AB 的距离为
,即点P到AB 的距离为