2024年高职单招《数学(中职)》每日一练试题12月08日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、直线3x+4y-5=0与圆x2+y2=1的位置关系是()
答 案:B
解 析:易得圆x2+y2=1的圆心为(0,0),半径r=1,则圆心(0,0)到直线3x+4y-5=0的距离d=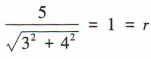 ,所以直线与圆相切.
,所以直线与圆相切.
2、已知甲组数据为10,11,12,13,14,乙组数据为11,12,12,12,13,设甲、乙的平均数分别为 ,甲、乙的方差分别为
,甲、乙的方差分别为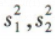 ,则下列说法正确的是()
,则下列说法正确的是()
答 案:C
解 析:易知甲的平均数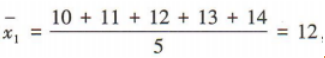 乙的平均数
乙的平均数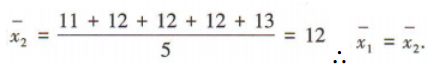 甲的方差
甲的方差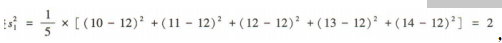 乙的方差
乙的方差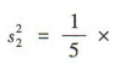
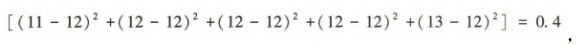

3、将图中所示的直角梯形ABCD绕AB所在的直线旋转一周,由此形成的几何体的体积是() 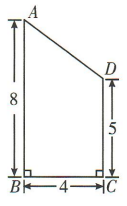
答 案:C
解 析:将题图中的直角梯形ABCD绕AB所在直线旋转一周可得上部分为圆锥,下部分为圆柱的组合体.易知圆锥的底面半径为4,高为3,圆柱的底面半径为4,高为5,所以该组合体的体积为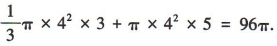
4、已知集合A={1,2,3},B={2,4},则A∩B=()
- A:∅
- B:{2}
- C:{1,3}
- D:{1,2,3,4}
答 案:B
解 析:易得集合A={1,2,3},B={2,4}中的所有公共元素为2,故A∩B={2}.
填空题
1、过直线2x-y+4=0与x-y+5=0的交点,且垂直于直线x-2y=0的直线的方程为()
答 案:2x+y-8=0
解 析:由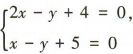 得
得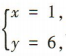 所以直线2x-y+4=0与x-y+5=0的交点为(1,6).因为垂直于直线x-2y=0的直线的斜率为-2,所以所求直线的方程为y-6=-2(x-1),即2x+y-8=0.
所以直线2x-y+4=0与x-y+5=0的交点为(1,6).因为垂直于直线x-2y=0的直线的斜率为-2,所以所求直线的方程为y-6=-2(x-1),即2x+y-8=0.
2、设函数f(x)=a2x-1+5,若f(2)=13,则f(-1)=()
答 案: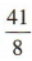
解 析:
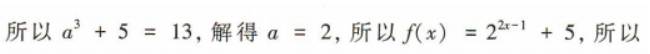
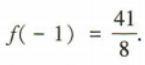
3、已知向量a,b满足|a|=1 ,且向量a与b的夹角为则(a+b)·(2a-b)=()
,且向量a与b的夹角为则(a+b)·(2a-b)=()
答 案:
解 析:

4、设集合A={-1,0,1,2},B={x l x2-4=0},那么AUB=()
答 案:{-2,-1,0,1,2}
解 析:因为A={-1,0,1,2},B=|x|x2-4=0}={-2,2},所以A∪B={-2,-1,0,1,2}.
简答题
1、已知在△ABC中,C为钝角,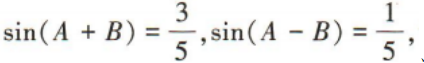 证明:tanA=2tanB
证明:tanA=2tanB
答 案: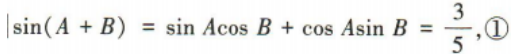
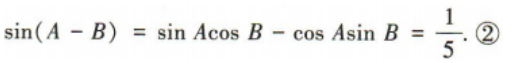

2、已知抛物线的顶点在原点,对称轴为y轴,焦点F(0,1).(1)求抛物线的标准方程;
(2)若过点A(0,m),且斜率为2的直线与该抛物线没有交点,求m的取值范围.
答 案:(1)设抛物线的标准方程为x2=2py,P >0. 由题意可得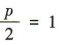 ,解得p= 2,
所以抛物线的标准方程为x2=4y.
(2)设过点A(0,m),且斜率为2的直线的方程为y=2x+m.
由
,解得p= 2,
所以抛物线的标准方程为x2=4y.
(2)设过点A(0,m),且斜率为2的直线的方程为y=2x+m.
由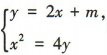 得x2-8x-4m=0.
因为直线与抛物线没有交点,
所以m=(-8)2-4(-4m)<0,解得m<-4.
所以m的取值范围是(-∞,-4).
得x2-8x-4m=0.
因为直线与抛物线没有交点,
所以m=(-8)2-4(-4m)<0,解得m<-4.
所以m的取值范围是(-∞,-4).
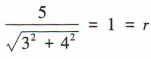 ,所以直线与圆相切.
,所以直线与圆相切. ,甲、乙的方差分别为
,甲、乙的方差分别为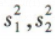 ,则下列说法正确的是()
,则下列说法正确的是()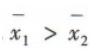
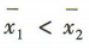
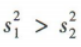
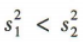
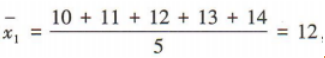 乙的平均数
乙的平均数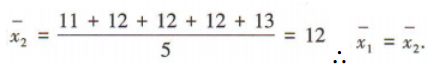 甲的方差
甲的方差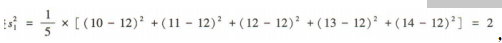 乙的方差
乙的方差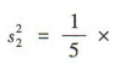
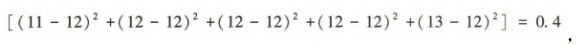


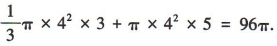
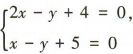 得
得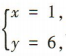 所以直线2x-y+4=0与x-y+5=0的交点为(1,6).因为垂直于直线x-2y=0的直线的斜率为-2,所以所求直线的方程为y-6=-2(x-1),即2x+y-8=0.
所以直线2x-y+4=0与x-y+5=0的交点为(1,6).因为垂直于直线x-2y=0的直线的斜率为-2,所以所求直线的方程为y-6=-2(x-1),即2x+y-8=0.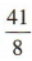

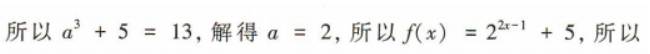
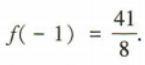
 ,且向量a与b的夹角为则(a+b)·(2a-b)=()
,且向量a与b的夹角为则(a+b)·(2a-b)=()



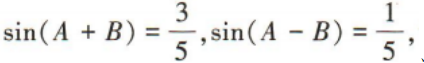 证明:tanA=2tanB
证明:tanA=2tanB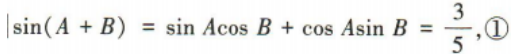
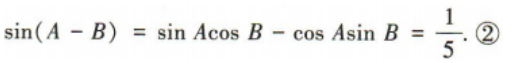

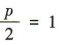 ,解得p= 2,
所以抛物线的标准方程为x2=4y.
(2)设过点A(0,m),且斜率为2的直线的方程为y=2x+m.
由
,解得p= 2,
所以抛物线的标准方程为x2=4y.
(2)设过点A(0,m),且斜率为2的直线的方程为y=2x+m.
由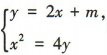 得x2-8x-4m=0.
因为直线与抛物线没有交点,
所以m=(-8)2-4(-4m)<0,解得m<-4.
所以m的取值范围是(-∞,-4).
得x2-8x-4m=0.
因为直线与抛物线没有交点,
所以m=(-8)2-4(-4m)<0,解得m<-4.
所以m的取值范围是(-∞,-4).



