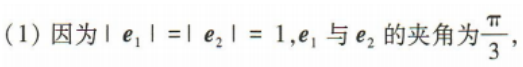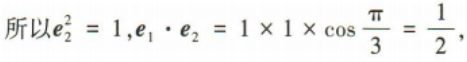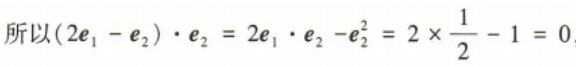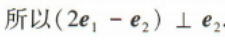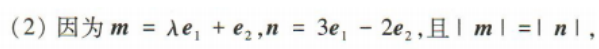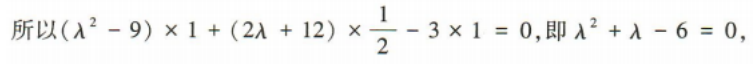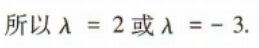2024年高职单招《数学(中职)》每日一练试题12月07日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、函数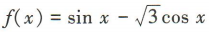 的最大值为()
的最大值为()
- A:1
- B:2
- C:
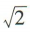
- D:
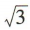
答 案:B
解 析:易知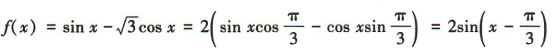 .因为
.因为 ,所以函数
,所以函数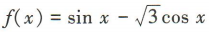 的最大值为2.
的最大值为2.
2、函数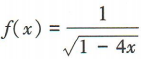 的定义域是()
的定义域是()
- A:[1,+∞]
- B:
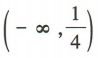
- C:
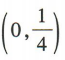
- D:(1,+∞)
答 案:B
解 析:要使函数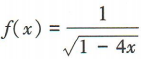 有意义,须
有意义,须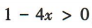 ,解得
,解得 ,故f(x)的定义域为
,故f(x)的定义域为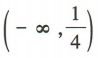 。
。
3、如图,在正方体ABCD-A1B1C1D1中,下列直线中与BD所成的角为60°的是()
答 案:D
解 析:在正方体ABCD-A1B1C1D1中,因为A1B1//AB,所以A1B1与BD所成的角为∠ABD.易知AB⊥AD,AB=AD,所以∠ABD=45°,所以A1B1与BD所成的角为45°,故A不符合题意.连接AC,因为A1A//C1C,且A1A=C1C,所以四边形A1ACC1为平行四边形,所以A1C1//AC,易知在正方形ABCD中,AC⊥BD,所以A1C1与BD所成的角为90°,故B不符合题意.因为A1A⊥平面ABCD,BD⊂平面ABCD,所以AA1⊥BD,所以AA1与BD所成的角为90°,故C不符合题意.连接B1D1,D1C.因为B1D1//BD,所以B1C与BD所成的角为∠D1B1C,易知B1D1=B1C=D1C,所以∠D1B1C=60°,所以B1C与BD所成的角为60°,故D符合题意.
4、已知集合A={x|-1≤x<2},B={y|y≤m},若A∪B=B,则m的取值范围是()
- A:{m|m<-1}
- B:{m|m≤-1}
- C:{m|m≥2}
- D:{m|m>2}
答 案:C
解 析:因为A∪B=B,所以 .又集合A={x|-1≤x<2},B={y|y≤m},所以m≥2,即m的取值范围是{m|m≥2}.
.又集合A={x|-1≤x<2},B={y|y≤m},所以m≥2,即m的取值范围是{m|m≥2}.
填空题
1、在正方体 ABCD-A1B1C1D1中,直线 A1B 与平面 ABCD 所成角的大小为()
答 案:45°
解 析:易得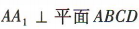 ,所以
,所以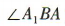 为A1B与平面ABCD所成的角.因为
为A1B与平面ABCD所成的角.因为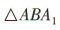 为等腰直角三角形,且
为等腰直角三角形,且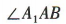 = 90°,所以
= 90°,所以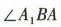 = 45°,所以直线 A1B 与平面 ABCD 所成的角为 45°.
= 45°,所以直线 A1B 与平面 ABCD 所成的角为 45°.
2、函数f(x)=sinxcosx+1的最小值为()
答 案:
解 析: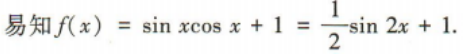

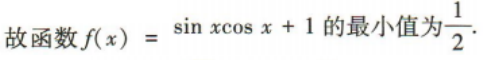
3、在△ABC中,内角A,B,C的对边分别为a,b,c,若a:b:c=3:2:4,则cosC的值为()
答 案:
解 析: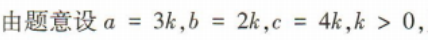
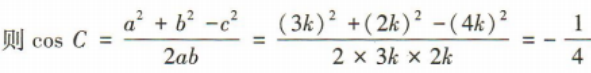
4、从一个12男11女的班级中任选一人进行问卷调査,抽到的是女同学的概率为()
答 案: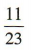
解 析:因为班级的人数为 12+11= 23,所以抽到的是女同学的概率为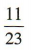
简答题
1、已知单位向量 (1)证明(2e1-e2)⊥e2;
(2)若
(1)证明(2e1-e2)⊥e2;
(2)若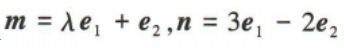 ,且|m|=|n|,求λ的值
,且|m|=|n|,求λ的值
答 案: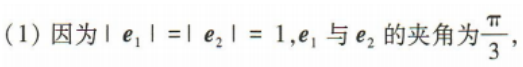
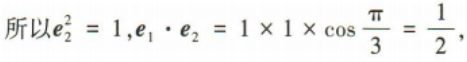
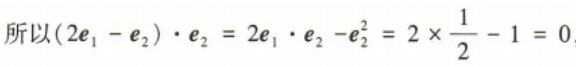
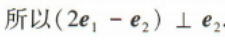
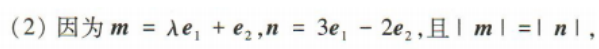

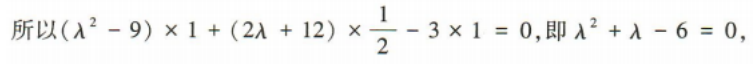
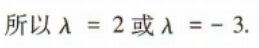
2、某工厂为了了解员工的工作效率,需调査 A,B,C三类工种的职工的工作情况,已知在该厂的全体职工中,A 工种占 40%,B工种占50%,C工种占 10%.现用分层抽样的方法从全体职工中抽取一个样本容量为n 的样本.(1)若n=200,则在A,B,C三类工种的职工中分别应抽取多少人?
(2)若抽取的A类工种的职工比C类工种的职工多 30 人,则抽取的B类工种的职工有多少人?
答 案:(1)若n=200,则在A类工种的职工中抽取的人数为 200x40%= 80.在B类工种的职工中抽取的人数为200x50%=100,在C类工种的职工中应抽取的人数为200x10%=20.
(2)若抽取的A类工种的职工比C类工种的职工多30人,则40%xn-10%xn=30,解得n=100,
所以抽取的 B类工种的职工的人数为100x50% =50.
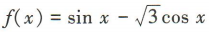 的最大值为()
的最大值为() 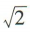
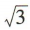
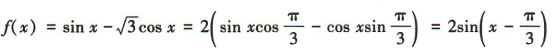 .因为
.因为 ,所以函数
,所以函数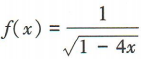 的定义域是()
的定义域是()
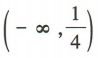
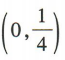
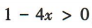 ,解得
,解得 ,故f(x)的定义域为
,故f(x)的定义域为
 .又集合A={x|-1≤x<2},B={y|y≤m},所以m≥2,即m的取值范围是{m|m≥2}.
.又集合A={x|-1≤x<2},B={y|y≤m},所以m≥2,即m的取值范围是{m|m≥2}.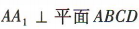 ,所以
,所以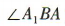 为A1B与平面ABCD所成的角.因为
为A1B与平面ABCD所成的角.因为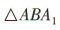 为等腰直角三角形,且
为等腰直角三角形,且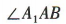 = 90°,所以
= 90°,所以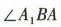 = 45°,所以直线 A1B 与平面 ABCD 所成的角为 45°.
= 45°,所以直线 A1B 与平面 ABCD 所成的角为 45°.
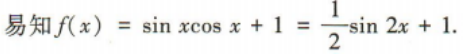

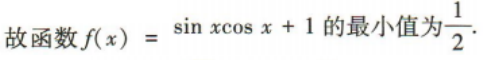

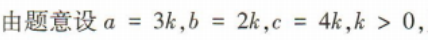
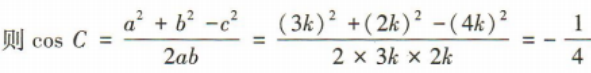
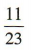
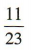
 (1)证明(2e1-e2)⊥e2;
(2)若
(1)证明(2e1-e2)⊥e2;
(2)若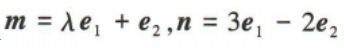 ,且|m|=|n|,求λ的值
,且|m|=|n|,求λ的值