2024年高职单招《数学(中职)》每日一练试题12月01日
2024-12-01 15:41:13 来源:吉格考试网
2024年高职单招《数学(中职)》每日一练试题12月01日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、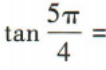 ()
()
- A:-1
- B:1
- C:
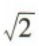
- D:
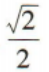
答 案:B
解 析: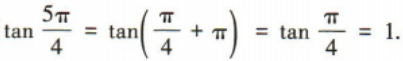
2、在四边形ABCD中,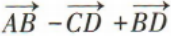 =()
=()
- A:
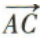
- B:
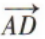
- C:
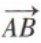
- D:

答 案:A
解 析: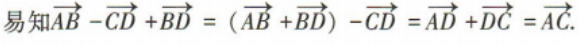
3、在正方体ABCD-A1B1C1D1中,直线A1C1与直线 A1B所成的角是()
- A:60°
- B:45°
- C:30°
- D: 15°
答 案:A
解 析:在正方体 ABCD-A1B1C1D1中,连接 C1B,如图.易得A1C1= A1B=C1B,所以 ΔA1BC1为等边三角形,所以∠C1A1B=60°,即A1C1与A1B所成的角为 60°. 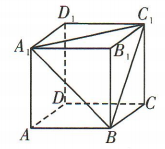
4、已知双曲线: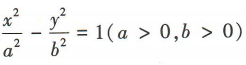 的一条渐近线与直线2x-y+3=0平行,则该双曲线的离心率是()
的一条渐近线与直线2x-y+3=0平行,则该双曲线的离心率是()
- A:
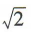
- B:
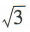
- C:2
- D:
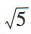
答 案:D
解 析:易知双曲线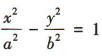 的渐近线方程为
的渐近线方程为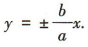 因为一条渐近线与直线2x-y+3=0,即y=2x+3平行,所以
因为一条渐近线与直线2x-y+3=0,即y=2x+3平行,所以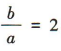 ,所以离心率
,所以离心率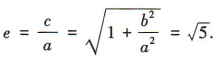
填空题
1、各棱长都为1的正三棱锥的体积是()
答 案: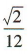
解 析:易知该正三棱锥的底面积为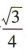 ,高为
,高为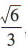 ,故该正三校锥的体积为
,故该正三校锥的体积为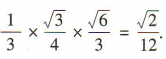
2、在正方体 ABCD-A1B1C1D1中,直线 A1B 与平面 ABCD 所成角的大小为()
答 案:45°
解 析:易得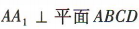 ,所以
,所以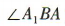 为A1B与平面ABCD所成的角.因为
为A1B与平面ABCD所成的角.因为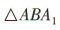 为等腰直角三角形,且
为等腰直角三角形,且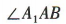 = 90°,所以
= 90°,所以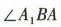 = 45°,所以直线 A1B 与平面 ABCD 所成的角为 45°.
= 45°,所以直线 A1B 与平面 ABCD 所成的角为 45°.
3、若全集U={0,1,2,3},集合P={2,3},则 ()
()
答 案:{0,1}
解 析:因为全集U={0,1,2,3},集合P={2,3},所以 ={0,1}.
={0,1}.
4、某机床生产一种零件,10天中,机床每天出的次品数分别是:0,1,0,2,2,0,3,1,2,4,则这10天中的次品数的中位数为()
答 案: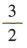
解 析:10天中的次品数由小到大排成一列为 0,0,0,1,1,2,2,2,3,4,所以这 10天中的次品数的中位数为
简答题
1、已知函数.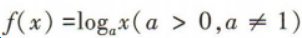 (1)若f(a)+f(2a)=3,求实数a的值;
(2)若
(1)若f(a)+f(2a)=3,求实数a的值;
(2)若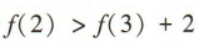 求实数a的取值范围.
求实数a的取值范围.
答 案: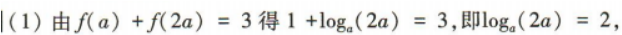
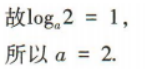
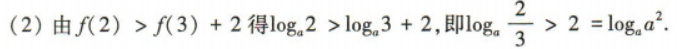
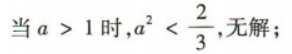
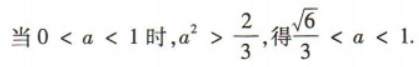

2、已知复数z满足z+|z|=1-2i,求复数z.
答 案:设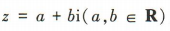 ,则
,则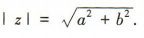 又z+lzl=1-2i,
所以
又z+lzl=1-2i,
所以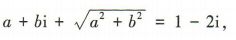 所以
所以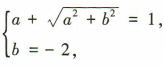 解得
解得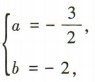 所以
所以