2024年高职单招《数学(中职)》每日一练试题11月30日

2024年高职单招《数学(中职)》每日一练试题11月30日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、在△ABC中，内角A,B,C的对边分别为a,b,c.若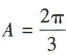,bc=3,且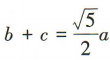,则a=()  

• A：
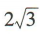
• B：
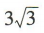
• C：
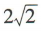
• D：

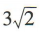
答 案：A

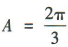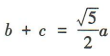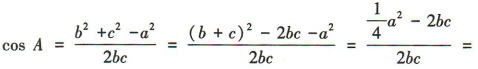
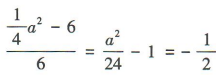解 析：因为,bc=3,且,所以,解得

2、已知A(-1,-1),B(1,3),C(x,5),若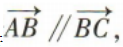则x=（）

• A：2
• B：-3
• C：-2
• D：5

答 案：A

解 析：

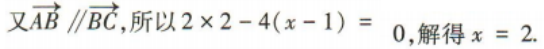
3、已知双曲线的焦距为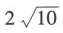,且双曲线的一条渐近线与直线3x+y=0垂直，则双曲线的方程为()  

• A：
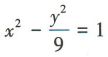
• B：
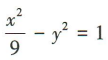
• C：
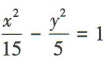
• D：

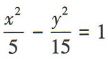
答 案：B

解 析：由双曲线的焦距为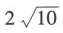得半焦距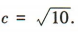因为双曲线的一条渐近线与直线3x+y=0垂直，且直线3x+y=0的斜率为-3,所以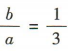,即a=3b.又a²+b²=c²,所以10b²=10,即b²=1,则a²=9,所以双曲线的方程为.

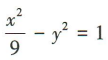4、已知抛物线的方程为y² =- 6x,过点(0,3)且倾斜角为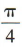的直线l交抛物线于A,B两点,则线段 AB的中点坐标为()  

• A：(-6,-3)
• B：(-3，-6)
• C：(6.3)
• D：(3,6)

答 案：A

解 析：因为直线l的倾斜角为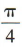,所以直线l的斜率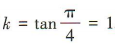.又直线l过点(0,3),所以直线l的方程为y=x+3.设A(x₁,y₁),B(x₂,y₂),线段AB的中点为N(x₀,y₀).由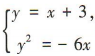得x²+12x+9=0,所以x₁+x₂=-12,所以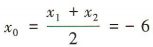,将x₀=-6代入y=x+3得y₀=-3,所以线段AB 的中点坐标为(-6,- 3).

填空题

1、设ω为实数，函数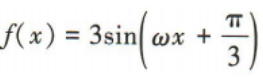的最小正周期为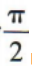则ω的值为（）

答 案：±4

解 析：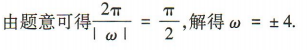

2、设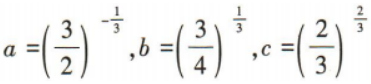则a,b,c的大小关系为.(用“＜”连接)

答 案：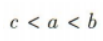

解 析：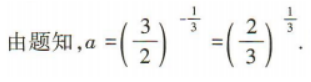

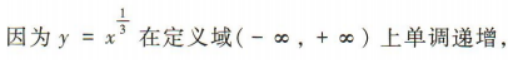
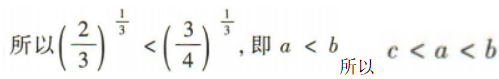
3、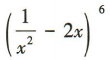的展开式中各项系数之和为()  

答 案：1

解 析：令x=1,得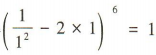,即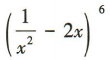的展开式中各项系数之和为1.

4、若函数y=2sinx+a的最大值为-2,则a的值为（）

答 案：-4

解 析：由-1≤sinx≤1,可知当sinx=1时，y=2sinx+a取得最大值2+a.由题意知2+a=-2,解得a=-4.

简答题

1、从含有2件次品的10件产品中随机抽取3件产品.求:(1)至多有1件次品的概率;
(2)至少有1件次品的概率.  

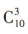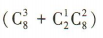答 案：从 10 件产品中任取3件,共有 种取法, (1)设A=“至多有一件次品”.由题意得从含有2件次品的 10件产品中随机抽取3件产品,至多有一件次品有种取法, 所以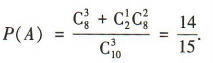 (2)设 B=“至少有一件次品”.由题意得从含有2件次品的 10件产品中随机抽取3件产品,至少有一件次品有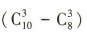种取法, 所以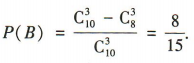  

2、在△ABC中，角A,B,C所对的边分别为a,b,c.若c=,b=1,C=120°,求： (1)角B; (2)△ABC的面积S.

答 案：