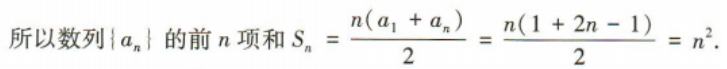2024年高职单招《数学(中职)》每日一练试题11月27日

2024年高职单招《数学(中职)》每日一练试题11月27日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、某校共有学生1200名,其中男生 700名,女生500名,为了解该校学生的安全意识情况,采用分层抽样方法,从全校学生中抽取 60 名进行调查,则应抽取的女生人数为()  

• A： 15
• B：20
• C：25
• D：30

答 案：C

解 析：易得抽样比例是所以应抽取的女生人数为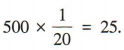

2、若直线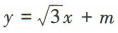与圆x²+y²-2y=0相切，则实数m的值为()  

• A：-1或3
• B：1或-3
• C：
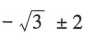
• D：55

答 案：A

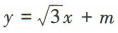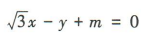解 析：x²+y²-2y=0可化为x²+(y-1)²=1,故圆的圆心为(0,1),半径为1,则圆心到直线即，即的距离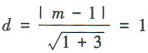,解得m=3或m=-1.

3、以(0,-1)为圆心,2为半径的圆的标准方程是（）  

• A：x²+(y+1)²=2
• B：x²+(y+1)²=4
• C：(x+1)²+y²=2
• D：(x+1)²+y²=4

答 案：B

解 析：以(0,-1)为圆心,2为半径的圆的标准方程是x²+(y+1)²=4.

4、函数的定义域是（）

• A：[2,+∞)
• B：(2,+∞)
• C：(-∞,2]
• D：(-∞,2)

答 案：A

解 析：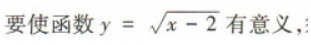

填空题

1、某学校三年级有8个班,甲、乙两人从外地转到该校三年级,学校让他们各自随机选择班级,他们刚好选在同一个班的概率为（）  

答 案：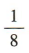

解 析：甲、乙两人各自随机选择班级,所有可能的情况有8²=64(种),而他们刚好选在同一个班的情况有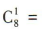8(种),故他们刚好选在同一个班的概率为

2、函数y=-x²+4x+1的单调递增区间是（）  

答 案：(-∞,2]

解 析：因为函数y=-x²+4x+1的图像开口向下，对称轴为直线x=2,所以该函数的单调递增区间为(-0,2]

3、某医疗机构有4名新冠疫情防控志愿者,现要从这4人中选3个人去3个不同的社区进行志愿服务则不同的安排方法共有（）种.  

答 案：24

解 析：由题意可分两步,第一步,从4名新冠疫情防控志愿者中选出3人,共有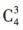种方法:第二步,选出的3人去3 个不同的社区,共有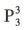种方法,根据分步乘法计数原理可知不同的安排方法共有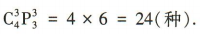

4、已知a=(1,2),b=(-2,2),且(ka+b)⊥(a-b),则k=（）  

答 案：2

解 析：因为a=(1,2),b=(-2,2),所以ka+b=(k-2,2k+2),a-b=(3,0).因为(ka+b)⊥(a-b),所以(ka+b)·(a-b)=3k-6=0,解得k=2.    

简答题

1、在等比数列{an}中,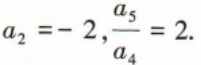 (1)求{an}的通项公式； (2)求数列{an}的前n项和Sn.

答 案：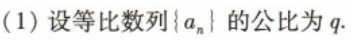

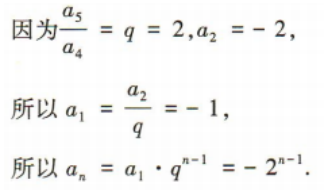
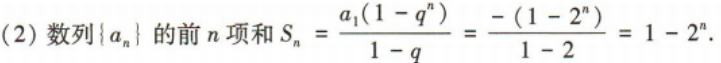
2、已知数列{a_n}中，a₁=1,a_n=2n-1. (1)证明{a_n}是等差数列； (2)求数列{a_n}的前n项和S_n.

答 案：(1)因为a_n+1-an=[2(n+1)-1]-(2n-1)=2,a1=1, 所以数列{a_n}是以1为首项，2为公差的等差数列.