2024年高职单招《数学(中职)》每日一练试题11月26日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、如果实数a,b满足a
答 案:B
解 析:由a0,所以 ,则
,则 ,故A不符合题意.由a
,故A不符合题意.由a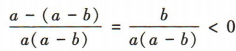 所以
所以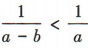 ,故B符合题意.由a,则a2>b2,即b2-a2<0,故C,D不符合题意.
,故B符合题意.由a,则a2>b2,即b2-a2<0,故C,D不符合题意.
2、已知f(x)为偶函数,且y=f(x)的图像经过点(2,-5),则下列等式恒成立的是()
- A:f(-5)=2
- B:f(-5)=-2
- C:f(-2)=5
- D:f(-2)=-5
答 案:D
解 析:由点(2,-5)在函数f(x)的图像上得f(2)=-5.因为f(x)是偶函数,所以f(-2)=f(2)=-5.
3、不等式 的解集为()
的解集为()
答 案:D
解 析:易知方程x2-6x+5=0的解分别为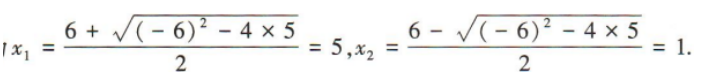


4、已知定义域为R的偶函数f(x)在(-∞,0)上单调递减,且f(2)=0,则满足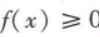 的x的取值范围是()
的x的取值范围是()
- A:(-∞,-2]∪[2,+∞)
- B:[-2,2]
- C:[-2,0)∪(0,2]
- D:[-2,0]∪[2,+∞)
答 案:A
解 析:∵f(x)为偶函数,且在(-∞,0)上单调递减,f(2)=0,∴f(-2)=0,且f(x)在(0,+∞)上单调递增,
填空题
1、若抛物线y=ax2-6x+c的开口向下,且与y轴交于正半轴,则抛物线的顶点位于第()象限.
答 案:二
解 析:因为抛物线y=ax2-6x+c的开口向下,且与y轴交于正半轴,
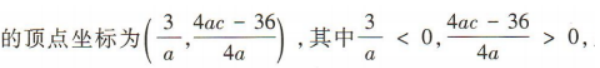 所以抛物线的顶点位于第二象限
所以抛物线的顶点位于第二象限
2、如图,画一个边长为4的正方形,再将这个正方形各边的中点相连得到第2个正方形,依此类推,这样一共画了10个正方形,则第10个正方形的面积为()

答 案: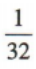
解 析:由题意知,第一个正方形的边长a1=4,面积T1=16;第二个正方形的边长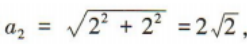 面积T2=8;第三个正方形的边长a3=2,面积T3=4;第四个正方形的边长
面积T2=8;第三个正方形的边长a3=2,面积T3=4;第四个正方形的边长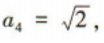 面积T4=2,……,由此可发现规律,第n个正方形的面积
面积T4=2,……,由此可发现规律,第n个正方形的面积
3、已知A(1,3),B(-2,-1),则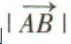 =()
=()
答 案:5
解 析: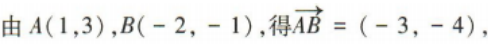

4、已知集合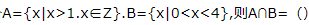
答 案:{2,3}
解 析: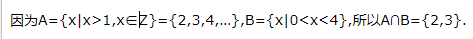
简答题
1、已知向量a=(1,x),b=(2x+3,-x).
(1)若a//b,求|a-b|;
(2)若a与b的夹角为锐角,求x的取值范围.
答 案:(1)因为a=(1,x),b=(2x+3,-x),a//b, 所以-x=x(2x+3),解得x=0或x=-2.
当x=0时,a=(1,0),b=(3,0),
所以a-b=(-2,0),
所以|a-b|=2;
当x=-2时,a=(1,-2),b=(-1,2),
所以a-b=(2,-4),
所以|a-b|=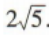 .
综上,|a-b|=2或Ia-bl=
.
综上,|a-b|=2或Ia-bl=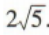 .
(2)由a与b的夹角为锐角,得a·b=2x+3-x2>0且-x≠x(2x+3),解得-1<x<3且x≠0,所以x的取值范围是(-1,0)∪(0,3).
.
(2)由a与b的夹角为锐角,得a·b=2x+3-x2>0且-x≠x(2x+3),解得-1<x<3且x≠0,所以x的取值范围是(-1,0)∪(0,3).
2、如图所示,在空间四边形ABCD中,E,F分别为AB,AD的中点,G,H分别在 BC,CD上,且BG:GC=DH:HC.证明E,F,G,H四点共面. 
答 案:∵BG:GC=DH:HC. ∴GH//BD.
∵E,F分别为 AB,AD 的中点,
∴EF//BD,
∴EF //GH.
∵过两平行直线有且只有一个平面,
∴E,F,G,H四点共面.

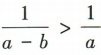

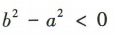
 ,则
,则 ,故A不符合题意.由a
,故A不符合题意.由a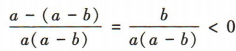 所以
所以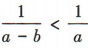 ,故B符合题意.由a
,故B符合题意.由a 的解集为()
的解集为()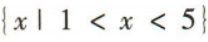

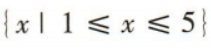

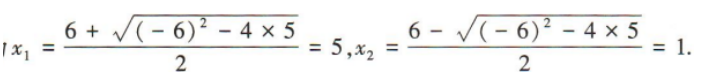


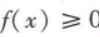 的x的取值范围是()
的x的取值范围是()

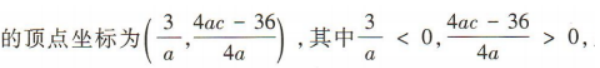 所以抛物线的顶点位于第二象限
所以抛物线的顶点位于第二象限
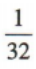
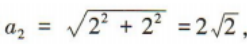 面积T2=8;第三个正方形的边长a3=2,面积T3=4;第四个正方形的边长
面积T2=8;第三个正方形的边长a3=2,面积T3=4;第四个正方形的边长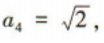 面积T4=2,……,由此可发现规律,第n个正方形的面积
面积T4=2,……,由此可发现规律,第n个正方形的面积
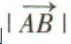 =()
=()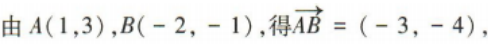

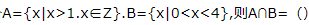
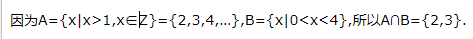
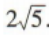 .
综上,|a-b|=2或Ia-bl=
.
综上,|a-b|=2或Ia-bl=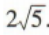 .
(2)由a与b的夹角为锐角,得a·b=2x+3-x2>0且-x≠x(2x+3),解得-1<x<3且x≠0,所以x的取值范围是(-1,0)∪(0,3).
.
(2)由a与b的夹角为锐角,得a·b=2x+3-x2>0且-x≠x(2x+3),解得-1<x<3且x≠0,所以x的取值范围是(-1,0)∪(0,3).



